Chapt 0: Starter

Feng Wan

wanfeng@xjtu.edu.cn

B832@仲英楼 or 3133@泓理楼 // School of Physcis @ Xian Jiaoton University

Contents

• 1 Applications
• 2 Other simulation examples
• 3 Computational Physcis

code.sourceCode {
  font-size: 5.0em;
}

1 Applications

1.1 Laser induced MD

顺反异构化

顺顺异构化

Figure 1: 激光脉冲引起的二苯乙烯分子的异构化反应的分子动力学模拟结果

蛋白质折叠的分子动力学模拟研究(314,000 atom simulation at UIUC)

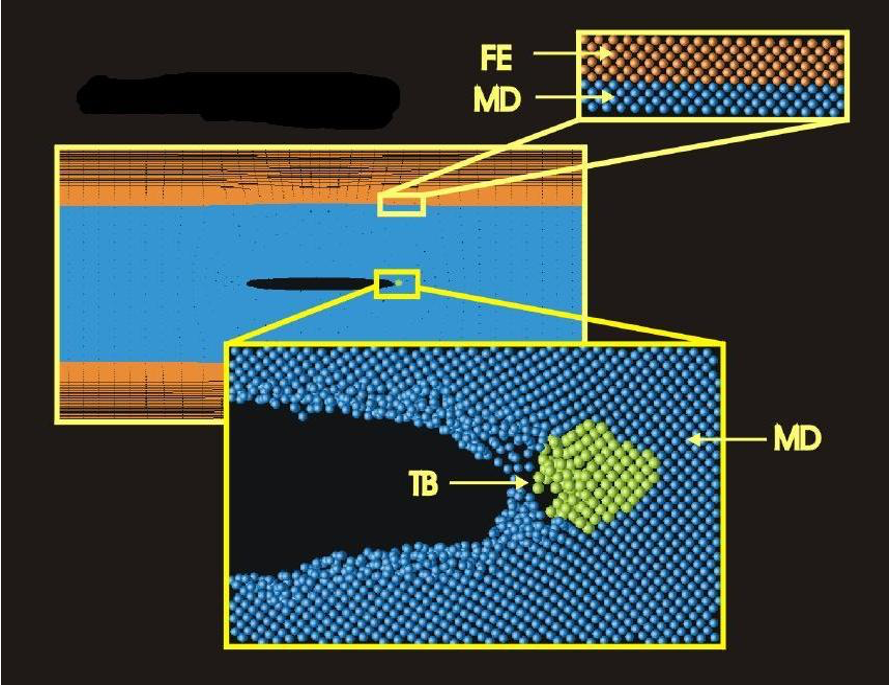
1.2 Silicon crystal defects

硅单晶中的断裂部位的传播(分子动力学)

Modeling materials on different length scales:

• quantum mechanics (tight binding)

• classical forces (molecular dynamics)

• continuum mechanics (finite element)

1.3 Neutron shelding via Monte Carlo

基于蒙特卡罗方法的中子屏蔽问题模拟

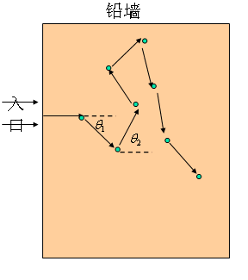
• 模型的建立
  假设铅墙厚度为5，中子在铅中的平均自由程为1，中子与铅原子碰撞后各向同性散射。令碰撞8次后中子能量耗尽
• 中子的水平位移\(S\)为
  \(1+ \cos\theta_1 + \cos\theta_2 +\cos\theta_3 +\cos\theta_4 +\cos\theta_5 +\cos\theta_6 +\cos\theta_7 +\cos\theta_8\)
• 当中子的水平位移\(S\)大于5时，中子则穿透了铅墙；小于0时，则表明中子反射回来了；位移S的值在0到5之间时，则表示中子被铅墙吸收了。

clear all
close all
clc
format long

    N=50000;
    x1=rand(1,N)*2*pi; %注意随机数要在计算函数值和误差，方差前给定
    x2=rand(1,N)*2*pi;
    x3=rand(1,N)*2*pi;
    x4=rand(1,N)*2*pi;
    x5=rand(1,N)*2*pi;
    x6=rand(1,N)*2*pi;
    x7=rand(1,N)*2*pi;
    s=1+cos(x1)+cos(x2)+cos(x3)+cos(x4)+cos(x5)+cos(x6)+cos(x7);

    N_1=0;
    N_2=0;
    N_3=0;
for i=1:N
    if s(i)<0      %计算被隔离墙反射的中子数目
        N_1=N_1+1;
    elseif s(i)>5     
        N_2=N_2+1; %计算穿过隔离墙的中子数目
    else
        N_3=N_3+1; %计算被隔离墙吸收的中子数目
    end
end
N_1/N
N_2/N  %计算穿过隔离墙的中子的比例
N_3/N
%figure;plot(1:N,x1/2/pi,'*')
%figure;plot(1:N,s,'*')
figure('Position', [100 100 1000 400]); 
subplot(121)
histogram(s, 100);
set(gca, 'fontsize', 18, 'linewidth', 1.5)
subplot(122)
[cy, cx] = histcounts(s, 100);
plot(cx(2:end), cy / N, 'k-', 'linewidth', 3);
hold on;
plot(cx(2:end), smooth(cy / N), 'r-', 'linewidth', 3);
set(gca, 'fontsize', 18, 'linewidth', 1.5)

1.3.1 python version

import numpy as np
import matplotlib.pyplot as plt
N = 5000000

data = np.random.rand(7, N)
s = np.sum(np.cos(data * 2.0 * np.pi), axis = 0) + 1.0

yy, xx = np.histogram(s, bins = 100)
dx = xx[1] - xx[0]
plt.plot(xx[1:] - 0.5 * dx, yy)

plt.fill_betweenx([0, yy.max()], xx[0], 0, color = 'red', alpha = 0.2)
plt.fill_betweenx([0, yy.max()], 0, 5, color = 'blue', alpha = 0.2)
plt.fill_betweenx([0, yy.max()], 5, xx[-1], color = 'green', alpha = 0.2)

n1 = np.sum(yy[xx[:-1] < 0])
n3 = np.sum(yy[xx[:-1] > 5])
n2 = np.sum(yy[np.logical_and(xx[:-1] >= 0, xx[:-1] <= 5)])

N = N * 1.0
plt.text(xx[0], yy.max() * 1.15, r'$n_1$ = %d, $n_2$ = %d, $n_3$ = %d' % (n1, n2, n3))
plt.text(xx[0], yy.max() * 1.1, r'$p_1$ = %4.3f, $p_2$ = %4.3f, $p_3$ = %4.3f' % (n1 / N, n2 / N, n3 / N))


plt.show()

1.4 Random walk (MC)

蒙特卡罗方法应用实例：随机行走问题

一醉汉从原点随机选择（上，下，左，右）方向开始移动，经过N步移动后（每步移动的距离为1），求距原点的距离

random-walk.m

clear all
close all
clc

N = 300;    % 每次行走步数为 N。
number=800;

step = [[1,0]; [-1, 0]; [0, 1]; [0, -1]];   % 可选的四种不同的位移矢量

for j=1:number
    zuobiao = [0, 0];       % 初始位置为原点
    for i = 1:N             % 行走 N 步
        k = ceil(4*rand()); % 随机选择方向 1、2、3、4，注意，ceil(x) 函数返回不小于 x 的最小整数，如 ceal（0.4）= 1.
        zuobiao = zuobiao + step(k,:);   %更新坐标，即在上一步坐标上加上位移矢量。
        %plot(0,0,'ro',zuobiao(1),zuobiao(2),'*')
    end
    hold on
    plot(0,0,'ro',zuobiao(1),zuobiao(2),'*')
end
   % r = norm(zuobiao)
   

import numpy as np
import matplotlib.pyplot as plt
N = 300
number = 800
step = np.reshape(np.array([1, 0, -1, 0, 0, 1, 0, -1]), [4, 2])
for i in range(number):
    position = np.array([0, 0])
    for j in range(N):
        k = np.floor(4.0 * np.random.rand())
        position = position + step[np.int64(k)]
    plt.plot(position[0], position[1], 'ro')
plt.show()

2 Other simulation examples

2.1 Black hole accretion

2.2 Proton-Proton scattering

2.3 Helmholtz instability

2.4 Wakefield acceleration

2.5 Quantum scattering

See more: https://github.com/quantum-visualizations/qmsolve.git

How to run the code:

1. pip install qmsolve
2. python examples/xxx.py

2.6 Ising model

See more: http://mattbierbaum.github.io/ising.js/

3 Computational Physcis

以计算机及计算机技术为工具和手段，运用计算科学所提供的各种方法，解决复杂物理问题的一门应用科学

3.1 History

• 20世纪40年代初，二战时期核武器研制中涉及的复杂问题，使得计算机介入物理学的研究在所难免

• 计算机的飞速发展

• 为报导计算物理领域的研究成果，召开学术会议、出版发行学术期刊
• 1963年 Livermore实验室的Berni & Alder编辑出版 Methods in Computational physics
• 1966年 美国的 Berni & Alder 主编创刊 Journal of Computational physics
  
• 1969年 英国的 Burki 主编在西欧创刊 Computer physics Communication
• 1984年9月中国出版《计算物理》杂志

3.2 Contents and methods

• Programming language
• Algorithms
• Program design
• Computer solving

Note

采用计算科学的方法，应用大规模高速计算机作为工具，解决理论或实验物理范畴内极其复杂的问题。

• TheoPhys …

• ExpPhys …

1. 研究首要问题是建立起相应的物理、数学模型，选择算法并使之可在计算机上实现 \[I(x) = \int_a^b \exp\left(-x^2\right)dx\] \[\frac{2}{\pi}\int_1^\infty e^{-\xi^2}d\xi = 0.1573\]

2. 第二个问题是算法的误差问题 (Error)

   • 模型误差 —— 次要因素的忽略、各种限制等
   • 观测误差 —— 模型中常包含一些通过实验测量而获得的物理参数。 如：比重、比热等等
   • 方法误差 —— 数学模型一般相当复杂，不能获得其精确解，或有些运算只能用极限过程定义，而计算机 只能进行有限次运算(截断误差) \[e^x = \sum_{n=0}^\infty \frac{x^n}{n!} ~~~ S_n(x) = \sum_{i=0}^\infty \frac{x^i}{i!}\] \[ R_n(x) = \frac{x^{n+1}}{(n+1)!}e^{\theta x}~~ 0<\theta<1\]
   • 舍入误差 —— 计算机的有限字长(计算误差)

3. 最后一个问题是计算的收敛性和稳定性问题 (Convergence & Stability)

Caution

• 收敛性主要研究算法误差的变化问题，而稳定性则更关注于舍入误差的问题 (round-off error)

• 如何评价一个算法的好坏

  • 计算结果的精度，即误差大小
  • 得到结果需要付出的代价 – 时空复杂性

3.3 References

• 主要参考教材：《计算物理学》 [美] Steven E.Koonin 著 秦克诚 译 高等教育出版社
• 参考书:
  • 《计算物理学》，顾昌鑫，复旦大学出版社
  • 《An Introduction to Computational Physics》,Tao Pang, Cambridge University Press
  • 《精通Matlab R2011a》, 张志涌，北京航空航天大学出版社。
  • 《计算机模拟方法在物理学中的应用》，Harvey Gould等，高等育出版社
  • 《计算物理基础》，彭芳麟，高等教育出版社

3.4 Course Information

• 教师：弯峰 赵前 徐忠锋 栗建兴

• 助教：任泳峥 负责《思源学习空间》课程资源建设与维护

• contacts:

  • 弯 峰: 157 7191 0192
  • 赵 前: 189 3031 8061
  • 徐忠锋: 133 0929 8803
    
  • 栗建兴: 151 2927 3796
    
  • 任泳峥: 123456

• tasks:
  • 课堂布置：算法巩固与应用
  • 算例：3/5（5个任选2个，第十周上课前向老师报备）

3.5 Contacts

• website: http://ispace.xjtu.edu.cn/course/18331/content#/
• QQ group: 720257508

3.6 Evaluation

Categories	Ratio	Remarks
Exercise	20%	Homework
Regular performance	10%	course
Seminar	20%	2/5
Thesis	50%	Free

Note

• Homework — 以常用算法训练为主
• Seminar — 每位同学1次课堂算例展示
• Thesis — 每算例/大作业最多可3人合作，老师首先评定算例/大作业得分，即首位得分，排第2减5分，第三减10分；也可根据同学们提交时同时按分工任务设定3人的比例。
  • 如某算例/大作业得分90分，3人得分分别为：方法一 90/85/80；方法二（假设比例为4:3:3）100/76.5/76.5

3.7 Course Plan

Chapter	Content	Course hours	Extra
0	Starter	2
1	Diff, Integral & Roots	5
2	IVP of ODE	5
3	BVP & EVP of ODE	6
4	PDE (Elliptic, Parabolic & Heli)	6
5	Monte Carlo	6
6	Molecule Dynamics	4

Topics in seminar:

• vibration energy level of two atoms molecule system
• orders and chaos in dynamics
• 1D schrödinger equation
• 1D t-d schrödinger equation
• 2D Ising model