1 Numerical solving the ODE
自然界中很多问题的描述,在数学中往往都归结为常微分方程的求解问题。
例如天文学中研究星体运动、空间技术中研究物体飞行、物理学中研究单摆的运动等,都需要求解常微分方程。
虽然求解微分方程有许多解析方法,但解析方法通常只能够求解一些特殊类型的方程或微分方程的一些特殊的情况。从实际意义上来讲我们更关心的是某些特定的自变量在某一个定义范围内的一系列离散点上的近似值。
单摆运动可以用如下常微分方程描述 \[ mL\ddot{\theta} = -mg\sin\theta \] for \(\theta \ll 5^\circ, ~~~ \Rightarrow \sin\theta \simeq \theta ~~ \Rightarrow\) \[\theta(t) = \theta_0 \sin(\omega t); ~~~ \omega = \sqrt{g/L}\]. 当 \(\theta_0\)很大时,上述常微分方程没有解析解,必须借助数值方法求解该方程,以描述单摆的运动。
一般地,\(n\) 阶常微分方程,通过引入若干辅助函数可以写成 \(n\) 个耦合的一阶常微分方程。
以物理学中常见的一个常微分方程(用于描述一维运动粒子)为例
\[\begin{eqnarray} m\frac{d^2 x}{dt^2}=f(x,t) ~~~ \Rightarrow ~~~ \left\lbrace\begin{matrix*}[l] \frac{dx}{dt} = \frac{p}{m} \\ \frac{dp}{dt} = f(x,t) \end{matrix*}\right. \end{eqnarray}\]一组\(M\)个耦合的一阶常微分方程可表示为
\[\frac{d\vec{y}}{dx} =\vec{f}(x,\vec{y})\] \(x\): variable, \(\vec{y}\) has \(M\) components.
因此,只要详细地讨论一阶常微分方程的数值方法即可! \[\frac{dy}{dx} =f(x, y)\] —
2 Classification of ODE
给定待求函数在某个初始点上的值
\[\begin{eqnarray} \left\lbrace\begin{matrix*} \frac{dy}{dx} = f(x, y) \\ y|_{x = a} = y_0 \end{matrix*}\right. \end{eqnarray}\]在自变量的两个端点上对待求函数施加约束,如函数值约束、导数值约束…
\[\begin{eqnarray} \left\lbrace\begin{matrix*} y''+\frac{\pi^2}{4}y+\frac{\pi^2}{4} = 0 \\ y(0) = 0, y(1) = 1 \end{matrix*}\right. \end{eqnarray}\]一类特殊的含有参数的边值问题。只有在参数取特定值时,方程才有非零解
\[\begin{eqnarray} \left\lbrace\begin{matrix*} \frac{d^2\varphi(x)}{dx^2} + k^2\varphi(x) = 0 \\ \varphi(0) = \varphi(1) = 0 \end{matrix*}\right. \end{eqnarray}\]3 初值问题的提法
\[ \begin{eqnarray} \left\lbrace\begin{matrix*} \frac{dy}{dx} = f(x, y) \\ y|_{x = a} = y_0 \end{matrix*}\right. ~~~ \Rightarrow ~~~ y = y(x), x\in[a, b] \end{eqnarray} \] 数值问题的提法:求节点\(x_k\)处的近似值\(y_k\) ,步长\(h_k= x_{k+1}- x_k\),为了方便,常取\(h\)不变,这样 \(N=(b-a)/h\)。
离散化:将区间 \([a, b]\) 分为 \(N\) 个等间隔的子区间,每个区间宽度为 \(h=(b-a)/N\).
寻找一个递推关系: 把 \(yn\) 同 \(\{y_{n-1}, y_{n-2}, …\}\) 联系起来。
4 Simple method
Show the code
\[f{\left(h + x_{0} \right)} = f{\left(x_{0} \right)} + h \left. \frac{d}{d \xi_{1}} f{\left(\xi_{1} \right)} \right|_{\substack{ \xi_{1}=x_{0} }} + \frac{h^{2} \left. \frac{d^{2}}{d \xi_{1}^{2}} f{\left(\xi_{1} \right)} \right|_{\substack{ \xi_{1}=x_{0} }}}{2} + \frac{h^{3} \left. \frac{d^{3}}{d \xi_{1}^{3}} f{\left(\xi_{1} \right)} \right|_{\substack{ \xi_{1}=x_{0} }}}{6} + O\left(h^{4}\right)\]
4.1 Euler method
Forward differential \(f'(x_0) = \frac{f(x_0 + h) - f(x_0)}{h} + O(h)\)
\[\Rightarrow f(x_0 + h) = f(x_0) + hf'(x_0) + O(h^2) \] \[\Rightarrow \begin{eqnarray} \left\lbrace\begin{matrix*}[l] y_{n+1} = y_n + hf(x_n, y_n) + O(h^2) \\ y(x_0) = y_0, ~~~ n = 1, 2, ..., N \end{matrix*}\right. \end{eqnarray} ~~~~~ ------ ~~~~~ \textrm{Euler method} \]
- 局部误差为 \(O(h^2)\)
- 全局误差为 \(NO(h^2) \approx O(h)\)
👎 精度太低!
👍 辅助理解常微方程初值问题数值解法的一些基本概念和构造方法
Show the code
from sympy import *
def ode(x, y):
return x**3 + 5 * x**2.0
# Euler method for solving ODE
def euler_method(ode, x0, y0, h, num_steps):
x_values = [x0]
y_values = [y0]
for _ in range(num_steps):
x = x_values[-1]
y = y_values[-1]
y_new = y + h * ode(x, y)
x_values.append(x + h)
y_values.append(y_new)
return x_values, y_values
# Initial conditions
x0 = -3
y0 = 1
h = 1
num_steps = 5
var('x')
var('y', cls = Function)
explicit = dsolve(Eq(Derivative(y(x), x), x**3 + 5 * x**2), y(x), ics={y(x0): y0})
call_fct = lambdify((x), explicit.rhs)
# Solve ODE using Euler method
x_values, y_values = euler_method(ode, x0, y0, h, num_steps)
# Plot the solution
plt.figure()
plt.plot(x_values, y_values, marker='o', color='b', label='Euler Method')
xx = np.linspace(x0, -x0, 100)
plt.plot(xx, call_fct(xx), color = 'r', label = 'Explicit')
plt.xlabel(r'$x$')
plt.ylabel(r'$y$')
plt.legend()
plt.grid(True)
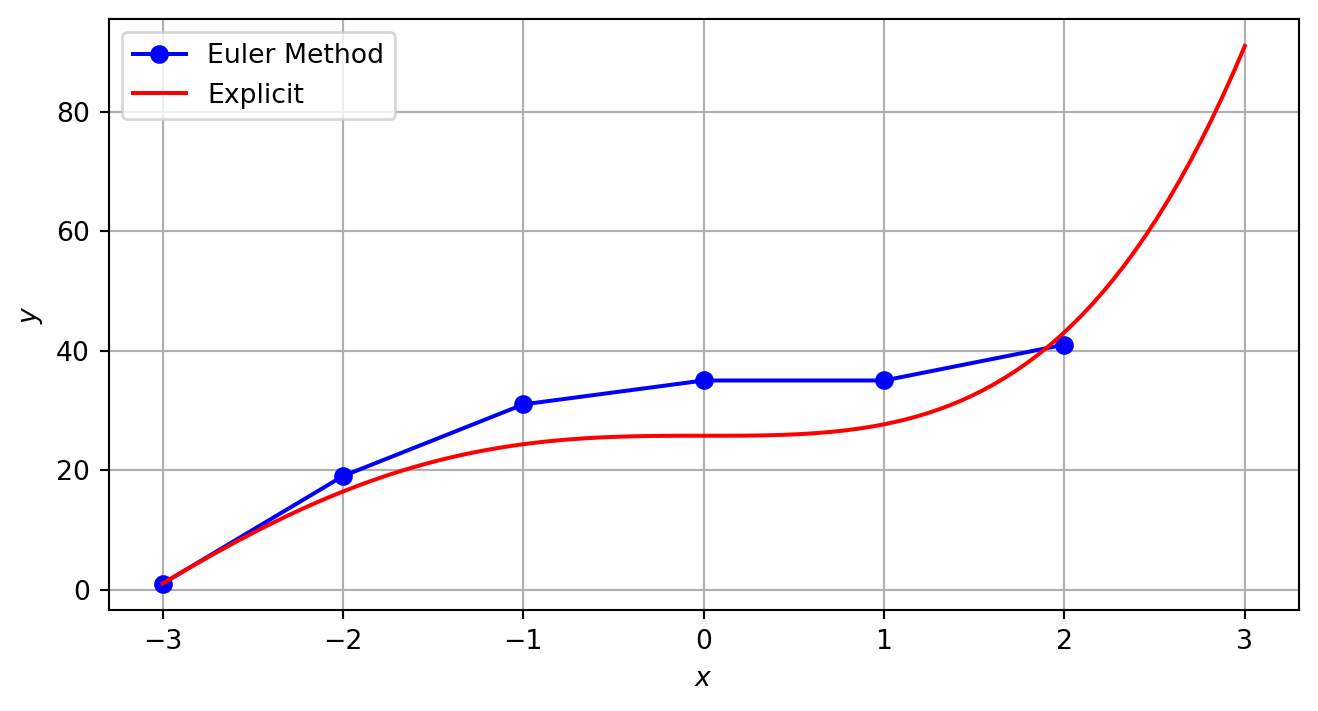
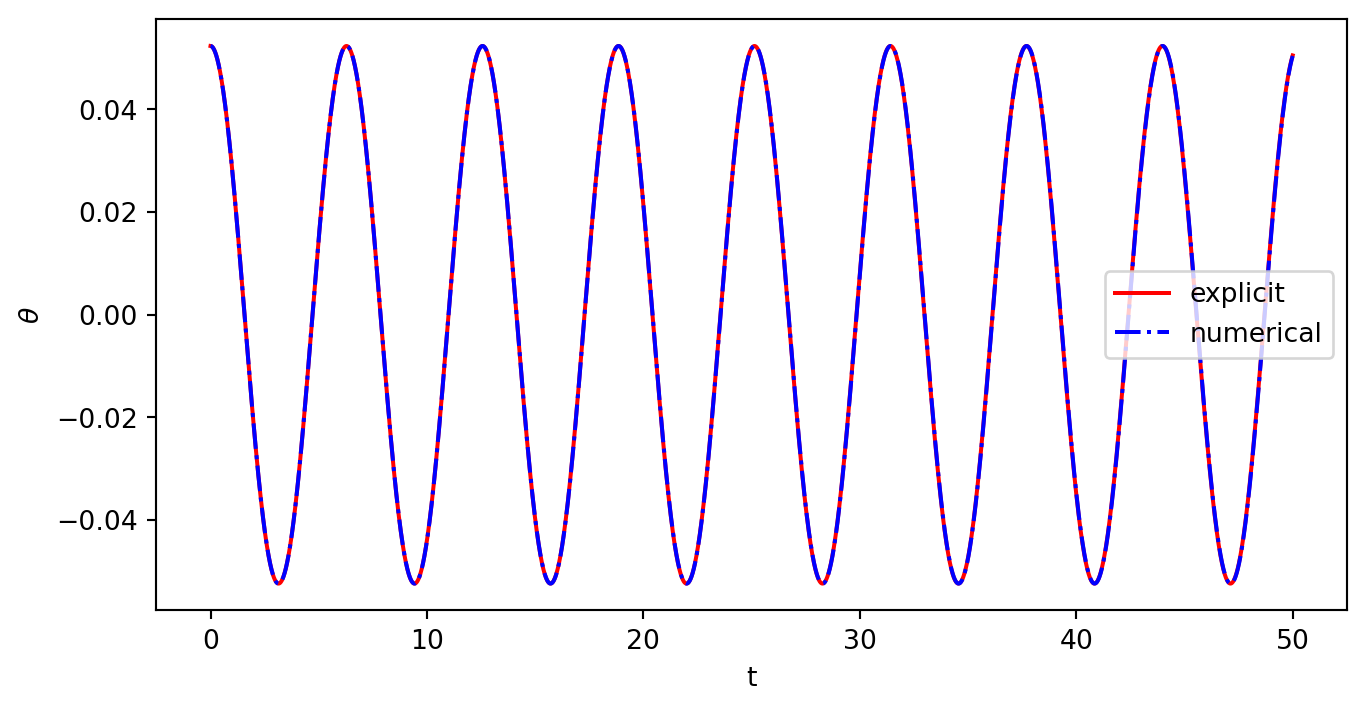
plt.show()Exercise 1 \(dy/dx = -xy; ~~~~ y(0) = 1\)
求\(y(1), ~y(3)\),对比不同步长\(h\);
\(y = e^{-x^2/2}\)
Solution 1.
Show the code
from sympy import *
from sympy.printing.mathml import print_mathml
from IPython.display import Markdown
result = dsolve(Eq(Derivative(y(x), x), -x*y(x)), y(x), ics={y(0): 1})
call_fct = lambdify((x), result.rhs)
def ode(x, y):
return - x * y
def euler(x0, y0, h, xp):
steps = int((xp - x0) / h)
yi = y0
xi = x0
for _ in np.arange(steps):
xi = xi + h
yi = yi + h * ode(xi, yi)
return xi, yi
hs = [0.5, 0.2, 0.1, 0.05, 0.02, 0.01, 0.005, 0.002, 0.001]
x0 = 0
y0 = 1
xp1 = 1
xp2 = 3
print('\t%s\t%s\t%s\t%s\t%s' %("h", "y(1)_n", "y(1)", "y(3)_n", "y(3)"))
for h in hs:
xp11, yp1 = euler(x0, y0, h, xp1)
xp22, yp2 = euler(x0, y0, h, xp2)
y1 = call_fct(xp1)
y2 = call_fct(xp2)
print("%6.4f\t%6.4f\t%6.4f\t%6.4f\t%6.4f" %(h, yp1, y1, yp2, y2))
plt.figure()
plt.plot(xx, call_fct(xx))
plt.show()
print('solution: ')
Markdown(f'$${latex( result )}$$') h y(1)_n y(1) y(3)_n y(3)
0.5000 0.3750 0.6065 0.0000 0.0111
0.2000 0.5223 0.6065 0.0018 0.0111
0.1000 0.5653 0.6065 0.0055 0.0111
0.0500 0.5861 0.6065 0.0080 0.0111
0.0200 0.5984 0.6065 0.0098 0.0111
0.0100 0.6025 0.6065 0.0105 0.0111
0.0050 0.6045 0.6065 0.0108 0.0111
0.0020 0.6057 0.6065 0.0110 0.0111
0.0010 0.6061 0.6065 0.0110 0.0111
solution: \[y{\left(x \right)} = e^{- \frac{x^{2}}{2}}\]
%filename: chapter2_example_1_Euler.m
% 求微分方程:Euler法
clear
clc
close all
x_in=3; %要求点的自变量值;
y=@(x)exp(-0.5*x.^2); %精确值
x=0:0.001:x_in;
h=0.01;
x0=0;
m=(x_in-x0)/h;
yy=zeros(1,m+1);
yy(1)=1; %初始条件;
for n=1:m %Euler method
xx(n)=x0+(n-1)*h;
yy(n+1)=yy(n)-h*xx(n)*yy(n);
end
xx(m+1)=x0+m*h;
plot(x,y(x),'r',xx,yy,'b')
legend('精确解','Euler法')
fprintf('y(x_in)的精确值为:%f\n',y(x_in));
fprintf('Euler法求得的值为:%f\n',yy(m+1));
error=y(x_in)-yy(m+1);
fprintf('Euler法误差为:%f\n',error);
4.2 Newton equation (2nd order ODE)
1D EOM for particle \(m\frac{dx^2}{dt^2} = f(x,t)\)
in Euler:
\[\begin{eqnarray} m\frac{d^2 x}{dt^2}=f(x,t) ~~~ \Rightarrow ~~~ \left\lbrace\begin{matrix*}[l] \frac{dx}{dt} = \frac{p}{m} \\ \frac{dp}{dt} = f(x,t) \end{matrix*}\right. \end{eqnarray} ~~~ \Rightarrow ~~~ \left\lbrace\begin{matrix*}[l] x_{n+1} = x_n + hp_n /m \\ p_{n+1} = p_n + hf(x_n,t_n) \end{matrix*}\right.\]%% matlab
for n = 1:N
x(n+1) = x(n) + h * p(n) /m
p(n+1) = p(n) + h * f(x(n), t(n))
endExercise 2 1D harmonic oscillator equation: \(m\ddot{x} = -kx\) with IC: \(x_0 = 5; p_0 = 0\)
✅ Explicit solution: \[ x = A\cos(\omega_0 t + \phi); ~~~ p = -mA\omega_0\sin(\omega_0t+\phi) \] with \(\omega_0 \equiv \sqrt{\frac{k}{m}}\).
\(A\) & \(\phi\) determined by IC:
\(\frac{1}{2}kx_0^2 + \frac{1}{2}mv_0^2 = \frac{1}{2}kA^2;~~~\phi=\cos^{-1}(x_0/A)\).
Solution 2.
Show the code
var('x', cls = Function)
var('t m k')
eqn = Eq(m * x(t).diff(t, 2) + k * x(t), 0)
ic = {x(0): 5, x(t).diff(t).subs(t, 0): 0, m: 1, k: 0.1}
result = dsolve(eqn).rhs
iceqn = [Eq(result.subs(t, 0), 5), Eq(result.diff(t).subs(t, 0), 0)]
icresult = solve(iceqn)
fin = result.subs(icresult[0]).subs(ic)
callct = lambdify((t), fin)
print('Equation: \n')
Markdown(f'$${latex(eqn)}$$')Equation:
\[k x{\left(t \right)} + m \frac{d^{2}}{d t^{2}} x{\left(t \right)} = 0\]
Solution:
\[x{\left(t \right)} = \frac{5 e^{0.316227766016838 i t}}{2} + \frac{5 e^{- 0.316227766016838 i t}}{2}\]
Show the code
P:
\[p{\left(t \right)} = 0.790569415042095 i e^{0.316227766016838 i t} - 0.790569415042095 i e^{- 0.316227766016838 i t}\]
Show the code
/Users/wanfeng/anaconda3/lib/python3.11/site-packages/matplotlib/cbook.py:1762: ComplexWarning:
Casting complex values to real discards the imaginary part
/Users/wanfeng/anaconda3/lib/python3.11/site-packages/matplotlib/cbook.py:1398: ComplexWarning:
Casting complex values to real discards the imaginary part
✅ Matlab
%filename: chapter2_example_2_harmonic_oscillator.m
%例题2:一维谐振子运动方程的数值求解
clear all
close all
clc
m=1; %谐振子质量
k=0.1;%弹簧劲度系数
h=0.0001; %时间步长,0.5,0.2,0.05
x0=5; %初始位置,可以任意设置
p0=0; %初始动量,可以任意设置
a=0; %时间起点
b=300; %时间终点
t=a:h:b;
N=(b-a)/h;
x=zeros(1,N+1);
p=zeros(1,N+1);
x(1)=x0;
p(1)=p0;
for n=1:N %Euler法迭代公式
x(n+1)=x(n)+h*p(n)/m;
p(n+1)=p(n)-h*k*x(n);
end
A=sqrt(x0^2+p0^2/(m*k)); %谐振子的振幅
pha=acos(x0/A); %谐振子的初始相位,若x0与p0同号,pha为负,否则pha为正
xx=A*cos(sqrt(k/m)*t+pha); %谐振子位置的精确解
pp=-m*A*sqrt(k/m)*sin(sqrt(k/m)*t+pha); %动量的精确解
EE=pp.^2/(2*m)+0.5*k*xx.^2; %能量的精确值
E=p.^2/(2*m)+0.5*k*x.^2; %能量的数值解
subplot(3,1,1),plot(t,x,'r',t,xx,'b')
title('谐振子的x(t)曲线')
subplot(3,1,2),plot(x,p,'r',xx,pp,'b')
title('谐振子的x-p相图')
subplot(3,1,3),plot(t,E,'r',t,EE,'b')
title('谐振子的能量随时间变化关系')4.3 Taylor series method
将 \(y_{n+1}\) 在 \(y_n\) 附近做泰勒展开
\[y_{n+1} = y(x_n+h) = y_n + hy'_n + \frac{1}{2}h^2y''_n+O(h^3)\] \[y'_n = f(x_n, y_n) \equiv f_n\] \[y''_n = \frac{d}{dx}f(x_n, y_n) = \frac{\partial f}{\partial x} + \frac{\partial f}{\partial y} \frac{\partial y}{\partial x} = \frac{\partial f}{\partial x} + \frac{\partial f}{\partial y} f \equiv f_x + f_y f\] \[\Rightarrow y_{n+1} = y_n + hf_n + \frac{1}{2}h^2[f_x + f_y f]_n + O(h^3) \tag{1}\]
局部误差为 \(O(h^3)\) 全局误差为 \(NO(h^3)\approx O(h^2)\)
这个公式在已知 \(f\) 的解析形式时很好用。阶数增大时,变得复杂。
3rd order of Taylor series?
\(y_{n+1} = y_n + ?\)
\[y_{n+1} = y(x_n + h) = y_n + hy'_n + \frac{1}{2}h^2y''_n + \frac{1}{6}h^3y'''_n+O(h^4)\]
\[y_{n+1} = y_n + hf_n + \frac{1}{2}h^2[f_x + f_yf]_n + \frac{1}{6}h^3[f_{xx}+2f_{xy}f+f_{yy}f^2 + f_y(f_x + f_y f)]_n + O(h^4) \tag{2}\]
Exercise 3 \[dy/dx = -xy;~~~~y(0) = 1\] 用Euler法与二阶泰勒级数法求解\(y(2)\)的值,采用不同的步长\(h\),并与精确值比较,计算误差大小。
Solution 3. \[y = e^{-x^2/2}\]
\[\begin{eqnarray} y_{n+1} &=& y_n + hf_n + \frac{1}{2}h^2[f_x + f_yf]_n+O(h^3) \\ & = & y_n - hx_n y_n + \frac{1}{2}h^2[-y_n + x_n^2y_n] +O(h^3) \end{eqnarray}\]%filename: chapter2_example_3_Euler_Taylor.m
% 例题3:求微分方程:Euler法and泰勒级数法
clear
clc;close all
format long
x_in=2; %要求点的自变量值
y=@(x)exp(-0.5*x.^2); %精确值
x=0:0.001:x_in;
h=0.1;
x0=0;
m=(x_in-x0)/h;
yy=zeros(1,m+1);
yy(1)=1;
for n=1:m %Euler method
xx(n)=x0+(n-1)*h;
yy(n+1)=yy(n)-h*xx(n)*yy(n);
end
xx(m+1)=x0+m*h;
yyy=zeros(1,m+1);
yyy(1)=1;
for n=1:m
yyy(n+1)=yyy(n)-h*xx(n)*yyy(n)+0.5*h^2*(-yyy(n)+xx(n)^2*yyy(n));
end
figure;plot(x,y(x),'r',xx,yy,'b',xx,yyy,'k') %画Euler法与泰勒级数法结果
legend('精确解','Euler法','泰勒级数法')
figure; plot(xx,y(xx)-yy,'r',xx,y(xx)-yyy,'b')
legend('Euler法','泰勒级数法')
fprintf('y(x_in)的精确值为:%f\n',y(x_in));
fprintf('Euler法求得的值为:%f\n',yy(m+1));
fprintf('泰勒级数法求得的值为:%f\n',yyy(m+1));
error=y(x_in)-yy(m+1);error1=y(x_in)-yyy(m+1);
fprintf('Euler法误差为:%f\n',error);
fprintf('泰勒级数法误差为:%f\n',error1);
Show the code
def taylor(x0, y0, h, xp):
steps = int((xp - x0) / h)
yi = y0
xi = x0
for _ in np.arange(steps):
xi = xi + h
yi = yi - h * xi * yi + 0.5 * h**2 * (-yi + xi**2 * yi)
return xi, yi
xp = 2
print('\t%s\t%s\t%s\t%s\t%s\t%s' %("h", "xp_e", "y(2)_e", "xp_t", "y(2)_t", "y(2)"))
for h in hs:
xp11, yp1 = euler(x0, y0, h, xp)
xp12, yp2 = taylor(x0, y0, h, xp)
y1 = call_fct(xp)
print("%6.4f\t%6.4f\t%6.4f\t%6.4f\t%6.4f\t%6.4f" %(h, xp11, yp1, xp12, yp2, y1)) h xp_e y(2)_e xp_t y(2)_t y(2)
0.5000 2.0000 0.0000 2.0000 0.0500 0.1353
0.2000 2.0000 0.0746 2.0000 0.0897 0.1353
0.1000 2.0000 0.1043 2.0000 0.1104 0.1353
0.0500 2.0000 0.1197 2.0000 0.1224 0.1353
0.0200 2.0000 0.1290 2.0000 0.1300 0.1353
0.0100 2.0000 0.1322 2.0000 0.1327 0.1353
0.0050 2.0000 0.1338 2.0000 0.1340 0.1353
0.0020 2.0000 0.1347 2.0000 0.1348 0.1353
0.0010 2.0000 0.1350 2.0000 0.1351 0.1353通常,建立微分方程的数值算法,有两条途径
用数值微分的两点公式 \(\frac{y_{n+1} - y_n}{x_{n+1} - x_n}\) 替代微分方程左边的一阶微商;如Euler法。
从\(x \rightarrow x+h\)积分恒等式\(y'(t)= f(t, y(t))\),得 \[y(x+k) - y(x) = \int_{x}^{x+h}f(t,y(t))dt\] i.e.
\[y_{n+1} - y_n = \int_{x_n}^{x_{n+1}}f(t,y(t))dt\]
5 Multiple step && Implicit method
5.1 Multiple step
\[y_{n+1} = y_n + \int_{x_n}^{x_{n+1}}f(t,y(t))dt\] Lagrange interpolation:
\[\begin{eqnarray} \varphi_1(x) &=& y_0 \frac{x - x_1}{x_0 - x_1} + y_1 \frac{x-x_0}{x_1 - x_0} \\ &=& y_{n-1} \frac{x-x_n}{x_{n-1}-x_n}+y_n\frac{x-x_{n-1}}{x_n - x_{n-1}} = -y_{n-1} \frac{x-x_n}{h} + y_n \frac{x-x_{n-1}}{h} \end{eqnarray}\]我们用 \(x_n\) 和 \(x_{n-}1\) 点上的 \(y\) 值来提供 \(f\) 在所需区间\([x_n , x_{n+1}]\)上的一个线性外插值,带入积分得
\[y_{n+1} = y_n + h(\frac{3}{2}f_n -\frac{1}{2}f_{n-1})+O(h^3)~~~---~~~\textrm{Adams-Bashforth 2-step method}\] with \(f_n \equiv f(x_n, y_n)\).
若以 \(f_n , f_{n-1}, f_{n-2} , f_{n-3}\) 的拟合多项式来外插(四次Lagrange插值), 得Adams-Bashforth四步法
\[y_{n+1} = y_n + \frac{h}{24}(55f_n - 59f_{n-1}+37f_{n-2}-9f_{n-3})+O(h^5)\] \[\varphi(x) = \sum_{j = 1}^k l_j(x)y_j + O(h^{k+1})\]
\[l_j(x) = \frac{(x-x_0)...(x-x_{j-1})(x-x_{j+1})...}{(x_j-x_0)...(x_j-x_{j-1})(x_j-x_{j+1})...}\]
Show the code
var('x x1 x2 x3 x4 h y1 y2 y3 y4')
var('f g', cls = Function)
f = y1*(x-x2)*(x-x3)*(x-x4)/((x1-x2)*(x1-x3)*(x1-x4)) + y2*(x-x1)*(x-x3)*(x-x4)/((x2-x1)*(x2-x3)*(x2-x4)) + y3*(x-x1)*(x-x2)*(x-x4)/((x3-x1)*(x3-x2)*(x3-x4)) + y4*(x-x1)*(x-x2)*(x-x3)/((x4-x1)*(x4-x2)*(x4-x3)) + Order(h)*h**4
Markdown(f'$${latex(Eq(g(x), f))}$$')\[g{\left(x \right)} = \frac{y_{4} \left(x - x_{1}\right) \left(x - x_{2}\right) \left(x - x_{3}\right)}{\left(- x_{1} + x_{4}\right) \left(- x_{2} + x_{4}\right) \left(- x_{3} + x_{4}\right)} + \frac{y_{3} \left(x - x_{1}\right) \left(x - x_{2}\right) \left(x - x_{4}\right)}{\left(- x_{1} + x_{3}\right) \left(- x_{2} + x_{3}\right) \left(x_{3} - x_{4}\right)} + \frac{y_{2} \left(x - x_{1}\right) \left(x - x_{3}\right) \left(x - x_{4}\right)}{\left(- x_{1} + x_{2}\right) \left(x_{2} - x_{3}\right) \left(x_{2} - x_{4}\right)} + \frac{y_{1} \left(x - x_{2}\right) \left(x - x_{3}\right) \left(x - x_{4}\right)}{\left(x_{1} - x_{2}\right) \left(x_{1} - x_{3}\right) \left(x_{1} - x_{4}\right)} + O\left(h^{5}\right)\]
\[g{\left(x \right)} = \frac{y_{4} \left(x - x_{1}\right) \left(- 2 h + x - x_{1}\right) \left(- h + x - x_{1}\right)}{6 h^{3}} - \frac{y_{3} \left(x - x_{1}\right) \left(- 3 h + x - x_{1}\right) \left(- h + x - x_{1}\right)}{2 h^{3}} + \frac{y_{2} \left(x - x_{1}\right) \left(- 3 h + x - x_{1}\right) \left(- 2 h + x - x_{1}\right)}{2 h^{3}} - \frac{y_{1} \left(- 3 h + x - x_{1}\right) \left(- 2 h + x - x_{1}\right) \left(- h + x - x_{1}\right)}{6 h^{3}} + O\left(h^{5}\right)\]
\[\frac{55 h y_{4}}{24} - \frac{59 h y_{3}}{24} + \frac{37 h y_{2}}{24} - \frac{3 h y_{1}}{8} + O\left(h^{5}\right)\]
单单关于\(y_0\)的值无法启动上述多步法,该方法的启动需要通过其他方法(如Euler法,泰勒级数法等)获得多个\(f\) 值。
Exercise 4 Adams-Bashforth 2-step method to solve (Exercise 3)
Solution 4.
%filename: chapter2_example_4_Adams_Bashforth.m
% 例题4,求微分方程:Adams-Bashforth二步法
clear all
clc
close all
x_in=2; %要求点的自变量值
y=@(x)exp(-0.5*x.^2); %精确值
x=0:0.001:x_in;
h=input('请输入步长h=');
x0=0;y0=1;
m=(x_in-x0)/h
yy=zeros(1,m+1);
xx=zeros(1,m+1);
xx(1)=x0; %第一个启动点
yy(1)=y0;
%下面调用Euler法与泰勒级数法,与上述AB二步法比较
ye=zeros(1,m+1);
yt=zeros(1,m+1);
ye(1)=1;
for n=1:m %Euler method
xx(n)=x0+(n-1)*h;
ye(n+1)=ye(n)-h*xx(n)*ye(n);
end
yt(1)=1;
for n=1:m
yt(n+1)=yt(n)-h*xx(n)*yt(n)+0.5*h^2*(-yt(n)+xx(n)^2*yt(n));
end
%用Euler法或泰勒级数法产生第二个启动点
xx(2)=x0+h;
yy(2)=yt(2); %精确值%yy(1)-h*xx(1)*yy(1); %第二个启动点
for n=2:m %Adams-Bashforth二步法
%xx(n)=x0+(n-1)*h;
yy(n+1)=yy(n)+h*(-1.5*xx(n)*yy(n)+0.5*xx(n-1)*yy(n-1));
end
xx(m+1)=x0+m*h;
figure;plot(x,y(x),'r',xx,ye,'b',xx,yt,'k',xx,yy,'g') %画Euler法,泰勒级数法与二步法结果
legend('精确解','Euler法','泰勒级数法','二步法')
figure; plot(xx,y(xx)-ye,'r',xx,y(xx)-yt,'b',xx,y(xx)-yy,'g')
legend('Euler法','泰勒级数法','二步法')
%plot(x,y(x),'r',xx,yy,'b')
%legend('精确解','Adams-Bashforth二步法')
fprintf('y(x_in)的精确值为:%f\n',y(x_in));
fprintf('Adams-Bashforth二步法求得的值为:%f\n',yy(m+1));
error=y(x_in)-yy(m+1);
fprintf('Adams-Bashforth二步法误差为:%f\n',error);
Show the code
def adams2step(x0, y0, h, xp):
steps = int((xp - x0) / h)
ym = y0
xm = x0
xi = x0 + h
yi = y0 + h * ode(x0, y0)
for _ in np.arange(steps - 1):
xi = xi + h
yp = yi + h * (1.5 * ode(xi, yi) - 0.5 * ode(xm, ym))
xm = xi
ym = yi
yi = yp
return xi, yi
xp = 2
print('\t%s\t%s\t%s\t%s\t%s\t%s' %("h", "xp_e", "y(2)_e", "xp_a", "y(2)_a", "y(2)"))
for h in hs:
xp11, yp1 = euler(x0, y0, h, xp)
xp12, yp2 = adams2step(x0, y0, h, xp)
y1 = call_fct(xp)
print("%6.4f\t%6.4f\t%6.4f\t%6.4f\t%6.4f\t%6.4f" %(h, xp11, yp1, xp12, yp2, y1)) h xp_e y(2)_e xp_a y(2)_a y(2)
0.5000 2.0000 0.0000 2.0000 -0.0156 0.1353
0.2000 2.0000 0.0746 2.0000 0.0915 0.1353
0.1000 2.0000 0.1043 2.0000 0.1110 0.1353
0.0500 2.0000 0.1197 2.0000 0.1225 0.1353
0.0200 2.0000 0.1290 2.0000 0.1300 0.1353
0.0100 2.0000 0.1322 2.0000 0.1327 0.1353
0.0050 2.0000 0.1338 2.0000 0.1340 0.1353
0.0020 2.0000 0.1347 2.0000 0.1348 0.1353
0.0010 2.0000 0.1350 2.0000 0.1351 0.13535.2 Implicit method
在区间$ [x_n , x_{n+1}] $上过 \(f_n, f_{n+1}\) 两点对 \(f\) 做线性插值,得 \[f = \frac{x-x_n}{h}f_{n+1} - \frac{x-x_{n+1}}{h}f_n+O(h^2)\] insert into the integral \(y_{n+1} = y_n + \int_{x_n}^{x_{n+1}} f(x, y)dx\) \[\Rightarrow ~~~ y_{n+1} = y_n + \frac{h}{2}[f(x_n,y_n)+f(x_{n+1},y_{n+1})] + O(h^3)\] 上式中等号两边都有\(y_{n+1}\)项,因此称为隐式法。
5.2.1 典型隐式法:Adams-Moulton二步法
Lagrange 二次插值:\(\varphi_2(x) = y_0l_0(x)+y_1l_1(x)+y_2l_2(x)\)
\(f\)采用此插值方法,从\(x_n\rightarrow x_{n+1}\)积分:
Show the code
\[g{\left(x \right)} = \frac{y_{3} \left(x - x_{1}\right) \left(x - x_{2}\right)}{\left(- x_{1} + x_{3}\right) \left(- x_{2} + x_{3}\right)} + \frac{y_{2} \left(x - x_{1}\right) \left(x - x_{3}\right)}{\left(- x_{1} + x_{2}\right) \left(x_{2} - x_{3}\right)} + \frac{y_{1} \left(x - x_{2}\right) \left(x - x_{3}\right)}{\left(x_{1} - x_{2}\right) \left(x_{1} - x_{3}\right)} + O\left(h^{4}\right)\]
\[g{\left(x \right)} = \frac{y_{3} \left(x - x_{2}\right) \left(h + x - x_{2}\right)}{2 h^{2}} - \frac{y_{2} \left(- h + x - x_{2}\right) \left(h + x - x_{2}\right)}{h^{2}} + \frac{y_{1} \left(x - x_{2}\right) \left(- h + x - x_{2}\right)}{2 h^{2}} + O\left(h^{4}\right)\]
Show the code
\[\frac{5 f_{2} h}{12} + \frac{2 f_{1} h}{3} - \frac{f_{0} h}{12} + O\left(h^{4}\right)\]
\[y_{n+1} = y_n + \frac{h}{12}(5f_{n+1}+8f_n-f_{n-1})+O(h^4)\]
\[y_{n+1} = y_n + \frac{h}{24}(9f_{n+1}+19f_n-5f_{n-1}+f_{n-2})+O(h^5)\]
Adams-Moulton二步法与三步法都既是多步法又是隐式法
多步法:最初几个格点的启动值需要通过其它的方法如欧拉法、泰勒级数法来获得
隐式法: 不能直接使用,它通常用在预报校正算法中
👍 先通过显式法“预报”一个\(y_{n+1}\)的值,然后利用隐式法来校正得到一个更精确的值。这样的算法有个优点,它可以持续监控积分的精度。
一个常常使用的具有局域误差 \(O(h^5)\) 的预报校正算法:
explicit Adams-Bashforth 4-step ✅ Adams-Moulton 3-step
隐式法意味着在每一个积分步都必须解一个方程,会非常耗时。
隐式算法的“预估-校正”思想可以帮助我们推导出著名的
6 Runge Kutta
隐式算法的预估-校正,多步法的启动都需要我们寻求一种高阶的单步算法。
要得到高阶方法的一个直接想法就是用Taylor展开,但这必须计算 \(y\) 的高阶微商,而一般情况下,求 \(f(x,y)\) 的微商相当麻烦,因此需寻求一种不求高阶微商的方法。
6.1 Start from Euler method:
\[\frac{dy}{dx} = f(x, y)\]
在子区间 \([x_n, x_{n+1}]\) 将微分方程写成积分形式
\[y_{n+1} = y_n + \int_{x_n}^{x_{n+1}}f(x, y)dx\]
\[\begin{eqnarray} \xRightarrow{\textrm{mean value theorem}} \left\lbrace\begin{matrix*}[l] y_{n+1} = y_n + h K_{avg} \\ K_{avg} = f(x_n + \theta h, y(x_n + \theta h)) \end{matrix*}\right. \end{eqnarray}\]欧拉法就是用 \(x_n\) 点的斜率近似 \([x_n, x_{n +1}]\)区间的平均斜率 \(K_{avg}\)
\[y_{n+1} = y_n + hf(x_n, y_n)\]
用 \(x_n, x_{n+1}\) 两点斜率\(K_1\)和\(K_2\)的平均值来近似区间\([x_n, x_{n+1}]\) 的平均斜率
\[y_{n+1} = y_n + \frac{h}{2}(K_1 + K_2)\]
\[\begin{eqnarray} \left\lbrace\begin{matrix*}[l] y_{n+1} = y_n + \frac{h}{2}(K_1 + K_2) \\ K_1 = f(x_n , y_n) \\ K_2 = f(x_n + h , \underbrace{y_n + hK_1}_{\text{Predicted}~~y_{n+1}}) \end{matrix*}\right. \end{eqnarray}\]但是由于 \(y_{n+1}\)待定,因此需要做“预报”,即“预估-校正”。
\[\star ~~~ y_{n+1} = y_n + \frac{h}{2}[f(x_n , y_n) + f(x_{n+1} , y_{n + 1})] + O(h^3) ~~~~ --- ~~~~ \textrm{Implicit method}\]
Combination of Euler && Implicit method
6.2 Further improvement?
\[\begin{eqnarray} \left\lbrace\begin{matrix*}[l] y_{n+1} = y_n + \frac{h}{2}\underbrace{(K_1 + K_2)}_{\text{what if not the mean value?}} \\ K_1 = f(x_n , y_n) \\ K_2 = f(x_n + \underbrace{h}_{\text{and no longer only one}~h} , y_n + hK_1) \end{matrix*}\right. \end{eqnarray}\]\[\Rightarrow~~~ \text{basic idea of \textcolor{red}{Runge Kutta}}\]
通过求不同点上的函数值,作线性组合,构造近似公式,把近似公式和解的Taylor展开式相比较,使其前面若干项相吻合,从而得到相应的高阶方法。
\[\Rightarrow ~~~ y_{n+1} = y_n + h\sum_{i=1}^n\lambda_iK_i ~~~~(\star)\]
with
\[\begin{eqnarray} \left\lbrace\begin{matrix*}[l] K_1 = f(x_n , y_n) = f_n \\ K_i = f(x_n + hc_i, y_n + hc_i\sum_{j=1}^{i-1}a_{ij}K_j) \end{matrix*}\right. ~~~~~ i =2,3,...,N \end{eqnarray}\]参数\(\lambda_i , c_i , a_{ij}\) 选取的原则是要求\((\star)\)的右端在\((x_n , y_n )\)处作Taylor展开后,按 \(h\) 的幂次重新整理
\[\tilde{y}_{n+1} = y_n + d_1h + \frac{1}{2!}d_2h^2+\frac{1}{3!}d_3h^3+...\] 与微分方程的解\(y(x)\)在\(x_n\)点处的Taylor展开式 \[y(x_n + h) = y(x_n) + hy'(x_n) + \frac{1}{2!}h^2y''(x_n)+... \tag{3}\] 有尽可能多的项重合。
以计算两个函数值的情况为例
\[y_{n+1} = y_n + h\sum_{i=1}^n\lambda_iK_i\]
Remark 1 (two points).
\[\begin{eqnarray} \left\lbrace\begin{matrix*}[l] y_{n+1} = y_n + h\lambda_1K_1 + h\lambda_2K_2 \\ K_1 = f(x_n , y_n) \\ K_2 = f(x_n + \underbrace{hc_2}_{\text{Taylor}}, y_n + \underbrace{hc_2a_{21}K_1}_{\text{Taylor}}) \end{matrix*}\right. \end{eqnarray}\]现在来确定\(\lambda_1 , \lambda_2 , c_2 , a_{21}\) \[K_1 = f_n = y'(x_n)\]
Remark 2. 二元函数的泰勒展开:
\[\begin{eqnarray} f(x_0 + h, y_0 + k) &=& f(x_0, y_0) + \left( h\partial_x+k\partial_y \right)f(x_0,y_0) \\ &+& \frac{1}{2!}\left( h\partial_x+k\partial_y \right)^2f(x_0,y_0) \\ &+& ... + \frac{1}{n!}\left( h\partial_x+k\partial_y \right)^nf(x_0,y_0) \\ &+&\frac{1}{(n+1)!}\left( h\partial_x+k\partial_y \right)^{n+1}f(x_0+\theta_h,y_0 + \theta_k) \end{eqnarray}\]with Remark 1 \[\Rightarrow ~~~ K_2 = f_n + hc_2(f_x + a_{21}ff_y)+O(h^2)\]
\[\begin{eqnarray} \Rightarrow ~~~ \tilde{y}_{n+1} &=& y_n + h\lambda_1K_1 + h\lambda_2K_2 \\ &=& y_n + h\lambda_1 f_n + h\lambda_2(f_n + hc_2(f_x + a_{21}ff_y)) + O(h^3) \\ &=& y_n + h(\lambda_1 + \lambda_2)f_n + h^2\lambda_2c_2(f_x+a_{21}ff_y)+O(h^3) \end{eqnarray}\]\[y''(x_n) = f'|_{(x_n,y_n)} = f_x + f_yf\] \(y(x_{n+1})\)在\(x_n\)处作Taylor展开 Equation 3
\[\Rightarrow ~~ \lambda_1 + \lambda_2 = 1, a_{21} = 1, \lambda_2c_2 = 1/2\]
Not unique ==>
\[\lambda_1 = \lambda_2 = 1/2, a_{21} = 1, c_2 = 1.\]
i.e. Euler法的梯形公式(2nd order Runge-Kutta method), see Tip 1, with truncation order of \(O(h^3)\).
Another choice:
\[\lambda_1 = 0, \lambda_2 = 1, a_{21} = 1, c_2 = 1/2.\]
\[\begin{eqnarray} \left\lbrace\begin{matrix*}[l] y_{n+1} = y_n + hK_2 + O(h^3) \\ K_1 = f(x_n , y_n) \\ K_2 = f\left(x_n + \frac{h}{2} , y_n + \frac{h}{2}K_1\right) \end{matrix*}\right. \end{eqnarray}\]Compare with the 2nd order Taylor series method (Equation 1).
6.3 3rd order Runge Kutta
\[\begin{eqnarray} \left\lbrace\begin{matrix*}[l] y_{n+1} = y_n + h\lambda_1K_1 + h\lambda_2K_2 + h\lambda_3K3 \\ K_1 = f(x_n , y_n)\\ K_2 = f(x_n +hc_2, y_n +hc_2a_{21}K_1)\\ K_3 = f(x_n +hc_3, y_n +hc_3a_{31}K_1+hc_3a_{32}K_2) \end{matrix*}\right. \end{eqnarray}\]Remember Remark 2
\[\begin{eqnarray} \Rightarrow ~~~ \left\lbrace\begin{matrix*}[l] K_2 = f_n + hc_2(f_x+a_{21}ff_y)+\frac{1}{2}h^2c^2[f_{xx}+a_{21}^2f_n^2f_{yy}+2a_{21}f_nf_{xy}]+O(h^3) \\ K_3 = f_n + hc_3(f_x+a_{31}ff_y + a_{32}K_2f_y)+\frac{1}{2}h^2c_3^2[f_{xx}+(a_{31}f+a_{32}K_2)^2f_{yy}+2(a_{31}f+a_{32}K_2)f_{xy}]+O(h^3) \end{matrix*}\right. \end{eqnarray}\]Compare with the Taylor expansion of \(y_{n+1}\) at \(x_n\):
\[ y_{n+1} = y_n + hf_n + \frac{1}{2}h^2[f_x+f_yf]_n + \frac{1}{6}h^3[f_{xx}+2f_{xy}f+f_{yy}f^2+f_y(f_x+f_yf)]_n+O(h^4) \]
\[\begin{eqnarray} \Rightarrow ~~~ \left\lbrace\begin{matrix*}[l] \lambda_1 + \lambda_2 + \lambda_3 = 1 \\ \lambda_2c_2 + \lambda_3c_3 = 1/2 \\ \lambda_2c_2a_{21} + \lambda_3c_3a_{31} + \lambda_3c_3a_{32} = 1/2 ... \end{matrix*}\right. \end{eqnarray}\]Choose:
\[\begin{eqnarray} \Rightarrow ~~~ \left\lbrace\begin{matrix*}[l] \lambda_1 = 1/6; ~~ \lambda_2 = 4/6; ~~\lambda_3 = 1/6 \\ c_2 = 1/2; ~~c_3 = 1; \\ a_{21} = 1; ~~ a_{31} = -1; ~~ a_{32} = 2 \end{matrix*}\right. \end{eqnarray}\]Remark 3 (3rd order Runge-Kutta method:).
\[\begin{eqnarray} \left\lbrace\begin{matrix*}[l] y_{n+1} = y_n + \frac{1}{6} h(K_1 + 4K_2 + K_3) \\ K_1 = f(x_n , y_n) \\ K_2 = f\left(x_n + \frac{h}{2} , y_n + \frac{h}{2}K_1\right) \\ K_3 = f\left(x_n + h , y_n + h(-K_1+2K_2)\right) \end{matrix*}\right. \end{eqnarray}\]Remark 4 (4th order Runge-Kutta method:).
\[\begin{eqnarray} \left\lbrace\begin{matrix*}[l] y_{n+1} = y_n + \frac{1}{6} h(K_1 + 2K_2 + 2K_3 + K_4) \\ K_1 = f(x_n , y_n) \\ K_2 = f\left(x_n + \frac{h}{2} , y_n + \frac{h}{2}K_1\right) \\ K_3 = f\left(x_n + \frac{h}{2} , y_n + \frac{h}{2}K_2\right) \\ K_4 = f(x_h + h, y_n + hK_3) \end{matrix*}\right. \end{eqnarray}\]- 龙格-库塔法的主要运算在于计算 \(K_i\) 的值,即计算 \(f\) 的值。Butcher 于1965年给出了计算量与可达到的最高精度阶数的关系:
| 每步须算\(K_i\) 的个数 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 可达到的最高精度 | \(O(h^2)\) | \(O(h^3)\) | \(O(h^4)\) | \(O(h^5)\) | \(O(h^6)\) | \(O(h^7)\) | \(O(h^8)\) |
- 由于龙格-库塔法的导出基于泰勒展开,故精度主要受解函数的光滑性影响。对于光滑性不太好的解,最好采用低阶算法而将步长\(h\) 取小。
Exercise 5 写出用4阶经典R-K法求初值问题
\[\begin{eqnarray} \left\lbrace\begin{matrix*}[l] y' = 8-3y \\ y_0 = y(0) = 2 \end{matrix*}\right. \end{eqnarray}\]的计算公式。并取步长 \(h=0.2\),计算\(y (0.4)\)的近似值
Solution 5.
Show the code
\[y{\left(x \right)} = \frac{8}{3} - \frac{2 e^{- 3 x}}{3}\]
Show the code
def ode(x, y):
res = 8.0 - 3.0 * y
return res
def rk4(func, x0, y0, h, xp):
steps = int((xp - x0) / h)
xi = x0
yi = y0
for _ in range(steps):
k1 = func(xi, yi)
k2 = func(xi + 0.5 * h, yi + 0.5 * h * k1)
k3 = func(xi + 0.5 * h, yi + 0.5 * h * k2)
k4 = func(xi + h, yi + h * k3)
xi = xi + h
yi = yi + h / 6.0 * (k1 + 2.0 * k2 + 2.0 * k3 + k4)
return xi, yi
hs = [0.2, 0.1, 0.05, 0.02]
print("\t h \tx \ty")
for h in hs:
xi, yi = rk4(ode, 0.0, 2.0, h, 0.4)
print("%6.4f\t%6.4f\t%6.4f" %(h, xi, yi)) h x y
0.2000 0.4000 2.4654
0.1000 0.4000 2.4658
0.0500 0.4000 2.4659
0.0200 0.4000 2.4659%filename: chapter2_example_5_RK.m
clear all
close all
clc
%比较Euler法与RK算法
format long
m=1.4;%input('请输入要求自变量点');
h=0.1;%input('请输入步长h=');
f = @(x,y)(8-3*y); % 定义 f
x=[0:h:m];
n=round(m/h);
y=zeros(1,n+1);
y(1)=2; %初始值
%4nd RK
for i=1:n
K1 =f(x(i), y(i));
K2 =f(x(i) + h/2, y(i) + h*K1/2 );
K3 =f(x(i) + h/2, y(i) + h*K2/2 );
K4=f(x(i) + h, y(i) + h*K3 );
y(i+1)=y(i) + 1/6*h*(K1 + 2*K2 + 2*K3 + K4 );
end
%Euler法
xx=[0:h:m];
yy=zeros(1,n+1);
yy(1)=2; %初始值
for i=1:n
yy(i+1)=yy(i)+h*(8-3*yy(i));
end
%%精确解
xxx=0:h:m;
yyy=@(xxx)8/3-2/3*exp(-3*xxx);
yyy(m)
error1=y(n+1)-yyy(m) %error of RK
error2=yy(n+1)-yyy(m) % Euler
plot(x,y,'-r',xx,yy,'-k',xxx,yyy(xxx),'b')
legend('RK方法','Euler法','精确解')
figure;plot(x,y-yyy(xxx),'-r')%,x,yy-yyy(xxx),'-b')
Exercise 6 例6 用Euler法、二阶泰勒级数法,Euler法的梯形公式以及经典四阶Runge-Kutta法分别求解下述常微分方程
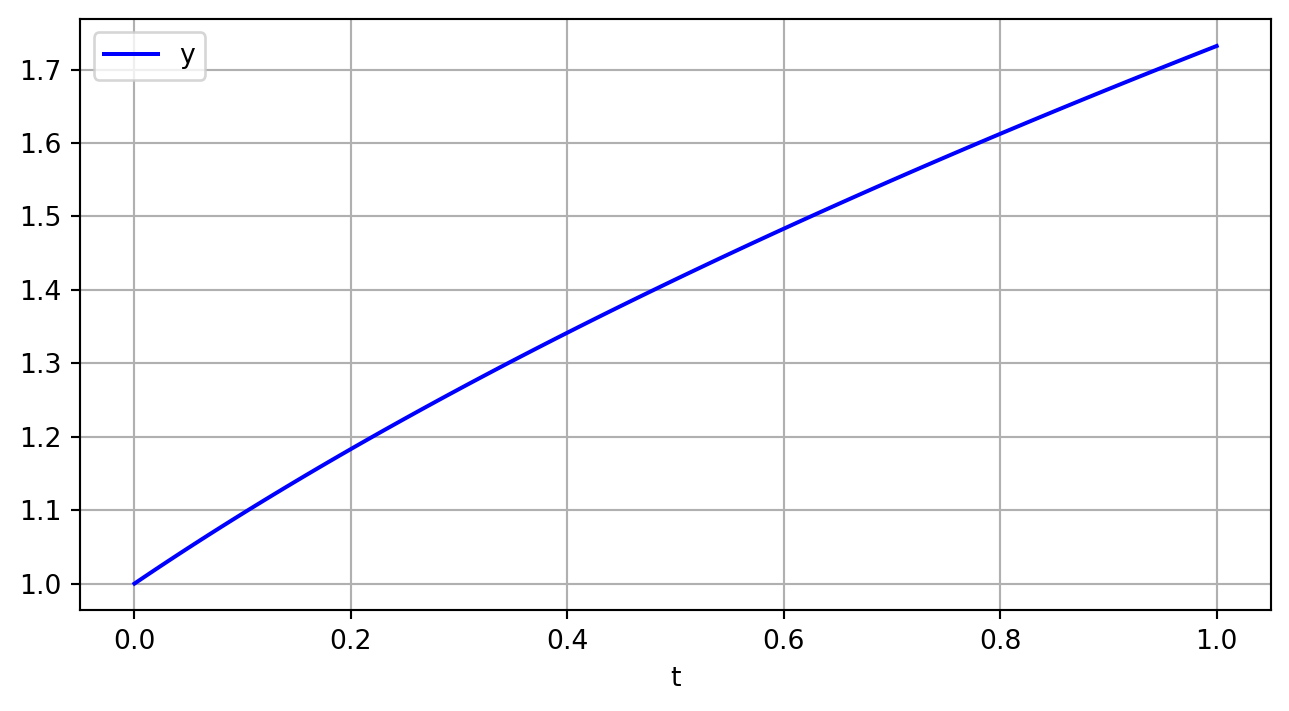
\[\begin{eqnarray} \left\lbrace\begin{matrix*}[l] y' = y - \frac{2x}{y} \\ y(0) = 1 \end{matrix*}\right. \end{eqnarray}\]的数值解,取\(h=0.1\),并与精确值比较。方程的解析解为: \(y = \sqrt{1+2x}\)
Solution 6.
%filename: chapter2_example_6_Euler_Taylor_Tri_RK.m
clear all
close all
clc
%比较Euler法、二阶泰勒级数法、Euler法的梯形算法与四阶RK算法-----
h=0.1; %step
x1=[0:h:1];
N=(max(x1)-min(x1))/h;
y0=1; %the initial value
f=@(x,y)(y-2*x/y);
%--------------解析解------------------------
y_e=sqrt(1+2*x1);
%----------Euler算法------------------------------
y_euler=zeros(1,N+1);
y_euler(1)=y0;
for n=1:N %Euler法迭代公式
y_euler(n+1)=y_euler(n)+h*(y_euler(n)-2*x1(n)/y_euler(n));
end
figure,subplot(2,1,1),plot(x1,y_e,'r',x1,y_euler,'b')
title('Euler法与精确结果比较图')
legend('精确解','Euler法结果')
subplot(2,1,2),plot(x1,abs(y_e-y_euler),'r')
title('Euler法与精确结果间的误差')
%----------二阶泰勒级数法----------
y_taylor=zeros(1,N+1);
y_taylor(1)=y0;
for n=1:N
y_taylor(n+1)=y_taylor(n)+h*(y_taylor(n)-2*x1(n)/y_taylor(n))...
+h^2/2*(-2/y_taylor(n)+(y_taylor(n)-2*x1(n)/y_taylor(n))*(1+2*x1(n)/y_taylor(n)^2));
end
%可见泰勒级数法比较复杂
figure,subplot(2,1,1),plot(x1,y_e,'r',x1,y_taylor,'b')
title('二阶泰勒级数法与精确结果比较图')
legend('精确解','二阶泰勒级数法结果')
subplot(2,1,2),plot(x1,abs(y_e-y_taylor),'r')
title('二阶泰勒级数法与精确结果间的误差')
%--------------改进的Euler法,二阶RK算法----------------
y_2rk=zeros(1,N+1);
y_2rk(1)=y0;
for n=1:N
k1=f(x1(n),y_2rk(n));
k2=f(x1(n)+h,y_2rk(n)+h*k1);
y_2rk(n+1)=y_2rk(n)+h/2*(k1+k2);
end
figure,subplot(2,1,1),plot(x1,y_e,'r',x1,y_2rk,'b')
title('二阶RK算法与精确结果比较图')
legend('精确解','二阶RK算法结果')
subplot(2,1,2),plot(x1,abs(y_e-y_2rk),'r')
title('二阶RK算法与精确结果间的误差')
%--------------4th RK算法------------------------
yy=zeros(1,N+1);
yy(1)=y0;
for n=1:N
k1=f(x1(n),yy(n));
k2=f(x1(n)+h/2,yy(n)+h/2*k1);
k3=f(x1(n)+h/2,yy(n)+h/2*k2);
k4=f(x1(n)+h,yy(n)+h*k3);
yy(n+1)=yy(n)+h/6*(k1+2*k2+2*k3+k4);
end
figure,subplot(2,1,1),plot(x1,y_e,'r',x1,yy,'b')
title('四阶RK算法与精确结果比较图')
legend('精确解','四阶RK算法结果')
subplot(2,1,2),plot(x1,abs(y_e-yy),'r')
title('四阶RK算法与精确结果间的误差')Show the code
\[y{\left(x \right)} = \sqrt{2 x + 1}\]
Show the code
h = 0.0100, xp = 1.0000, y_e = 1.7012, y_rk = 1.7321, y_real = 1.73216.4 High order ODE:
By introducing an auxiliry variable, transforms into 1-order ODE set:
e.g.
\[\begin{eqnarray} \left\lbrace\begin{matrix*}[l] \frac{dy}{dx} = f(x, y, z) \\ \frac{dz}{dx} = g(x, y, z), a\leq x \leq b \\ y(a) = y_0 \\ z(a) = z_0 \end{matrix*}\right. \end{eqnarray}\]Euler:
\[\begin{eqnarray} \left\lbrace\begin{matrix*}[l] y_{n+1} = y_n + hf(x_n, y_n, z_n) \\ z_{n+1} = z_n + hg(x_n, y_n, z_n) \end{matrix*}\right. \end{eqnarray}\]4th order RK:
\[\begin{eqnarray} \left\lbrace\begin{matrix*}[l] y_{n+1} \\ z_{n+1} \end{matrix*}\right\rbrace = \left\lbrace\begin{matrix*}[l] y_{n} \\ z_{n} \end{matrix*}\right\rbrace + \frac{h}{6}(K_1 + 2K_2 + 2K_3 + K4) \end{eqnarray}\]\[K_1 = \left\lbrace\begin{matrix*}[l] f(x_n, y_n, z_n) \\ g(x_n, y_n, z_n) \end{matrix*}\right\rbrace \]
\[K_2 = \left\lbrace\begin{matrix*}[l] f(x_n + \frac{h}{2}, y_n + \frac{h}{2}K_1^{(1)}, z_n + \frac{h}{2}K_1^{(2)}) \\ g(x_n + \frac{h}{2}, y_n + \frac{h}{2}K_1^{(1)}, z_n + \frac{h}{2}K_1^{(2)}) \end{matrix*}\right\rbrace \]
\[K_3 = \left\lbrace\begin{matrix*}[l] f(x_n + \frac{h}{2}, y_n + \frac{h}{2}K_2^{(1)}, z_n + \frac{h}{2}K_2^{(2)}) \\ g(x_n + \frac{h}{2}, y_n + \frac{h}{2}K_2^{(1)}, z_n + \frac{h}{2}K_2^{(2)}) \end{matrix*}\right\rbrace \]
\[K_4 = \left\lbrace\begin{matrix*}[l] f(x_n + h, y_n + hK_3^{(1)}, z_n + hK_3^{(2)}) \\ g(x_n + h, y_n + hK_3^{(1)}, z_n + hK_3^{(2)}) \end{matrix*}\right\rbrace \]
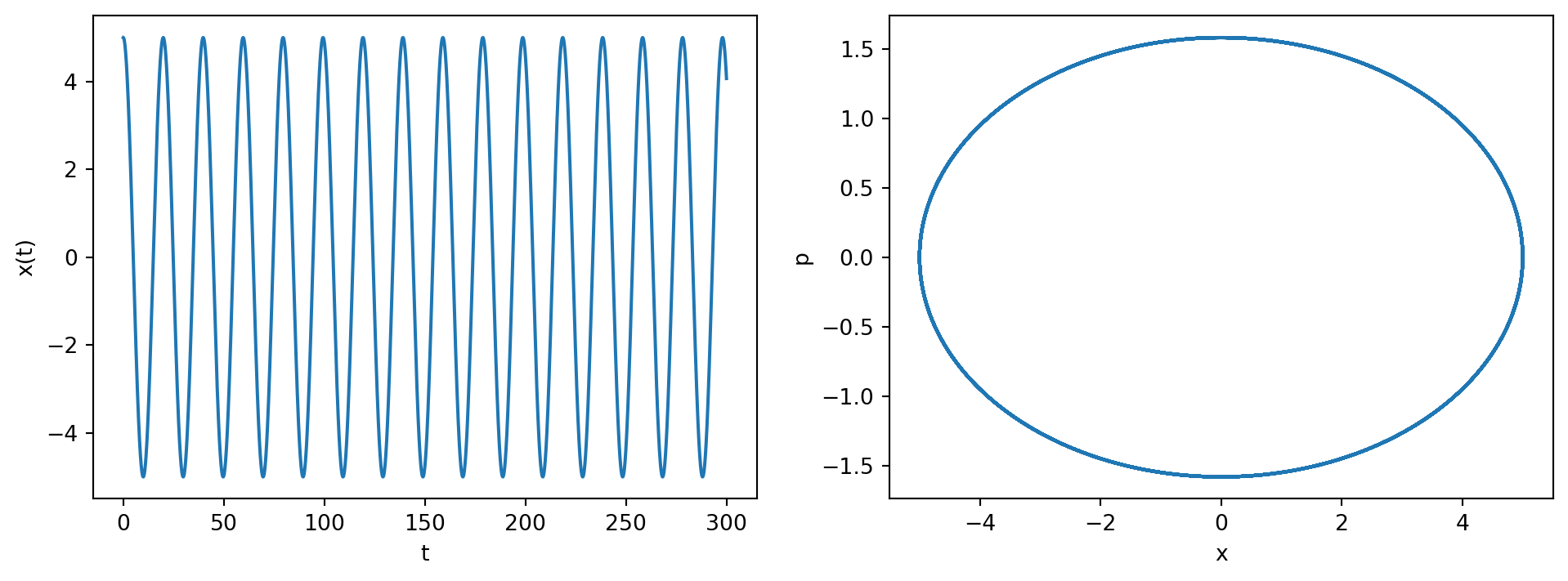
Exercise 7 \[\frac{dy}{dt} = p;~~\frac{dp}{dt}=-4\pi^2y\] 确定了周期为1的简谐振动;考察其演化过程。
Solution 7.
%filename: chapter2_example_7_erbianliang_RK_test_1.m
function two_variables_RK
clear all
close all
clc
%比较Euler法、四阶RK算法-----
time = 10; N = 40000;
h = time/N;
t = 0:h:time;
y0=5; %初始位置,可以任意设置
p0=0; %初始动量,可以任意设置
%--------------解析解------------------------
m=1; %谐振子的质量为1
k=4*pi^2; %弹簧的劲度系数
A=sqrt(y0^2+p0^2/(m*k)); %谐振子的振幅
pha=acos(y0/A); %谐振子的初始相位,若x0与p0同号,pha为负,否则pha为正
y_e=A*cos(sqrt(k/m)*t+pha); %谐振子的精确解
p_e=-m*A*sqrt(k/m)*sin(sqrt(k/m)*t+pha); %动量的精确解
E_e=p_e.^2/(2*m)+0.5*k*y_e.^2; %能量的精确值
E_e(1)
%----------Euler算法------------------------------
yyy=zeros(1,N+1);
ppp=zeros(1,N+1);
yyy(1)=y0;
ppp(1)=p0;
for n=1:N %Euler法迭代公式
yyy(n+1)=yyy(n)+h*ppp(n);
ppp(n+1)=ppp(n)-h*4*pi^2*yyy(n);
end
E_euler=ppp.^2/(2*m)+0.5*k*yyy.^2; %能量的数值解
figure,subplot(2,2,1),plot(t,yyy,'r',t,y_e,'b')
title('谐振子的位置(Euler算法与精确解比较)')
legend('Euler算法','精确解')
subplot(2,2,2),plot(t,ppp,'r',t,p_e,'b')
title('谐振子的动量(Euler算法与精确解比较)')
legend('Euler算法','精确解')
subplot(2,2,3),plot(yyy,ppp,'r',y_e,p_e,'b')
title('谐振子的相图(Euler算法与精确解比较)')
legend('Euler算法','精确解')
subplot(2,2,4),plot(t,E_euler-E_e,'r')
title('误差')
%--------------四阶RK算法------------------------
yy=zeros(1,N+1);
pp=zeros(1,N+1);
yy(1)=y0;
pp(1)=p0;
f=@(t,y,p)[p; -4*pi^2*y]; % 定义 f,写成列向量形式
z0 = [y0; p0]; %初始条件,y0=5,p0=0
z = myrungekutta(f, t, z0);
yy = z(1,:);
pp = z(2,:);
E_rk=pp.^2/(2*m)+0.5*k*yy.^2; %能量的数值解
figure,subplot(2,2,1),plot(t,yy,'r',t,y_e,'b')
title('谐振子的位置(四阶RK算法与精确解比较)')
legend('四阶RK算法','精确解')
subplot(2,2,2),plot(t,pp,'r',t,p_e,'b')
title('谐振子的动量(四阶RK算法与精确解比较)')
legend('四阶RK算法','精确解')
subplot(2,2,3),plot(yy,pp,'r',y_e,p_e,'b')
title('谐振子的相图(四阶RK算法与精确解比较)')
legend('四阶RK算法','精确解')
subplot(2,2,4),plot(t,E_rk(1,:)-E_e,'r')
title('误差')
function z= myrungekutta(f, t, z0)
n = length(t);
h = t(2)-t(1);
z=zeros(2,n);
%定义一个2行n列的数组,2为未知数的个数,也即方程组中方程的个数
z(:,1)=z0;
for i = 1:n-1
k1=f(t(i), z(1,i),z(2,i));
k2=f(t(i)+0.5*h, z(1,i) + h*k1(1)/2, z(2,i) + h*k1(2)/2);
k3=f(t(i)+0.5*h, z(1,i) + h*k2(1)/2, z(2,i) + h*k2(2)/2);
k4=f(t(i)+h, z(1,i) + h*k3(1), z(2,i) + h*k3(2));
z(1,i+1)=z(1,i) + h*(k1(1) + 2*k2(1) + 2*k3(1) + k4(1))/6;
z(2,i+1)=z(2,i) + h*(k1(2) + 2*k2(2) + 2*k3(2) + k4(2))/6;
end
Show the code
\[\left[ y{\left(t \right)} = \frac{\sin{\left(2 \sqrt{\pi} t \right)}}{2 \sqrt{\pi}}, \ p{\left(t \right)} = \cos{\left(2 \sqrt{\pi} t \right)}\right]\]
Exercise 8 已知两个耦合的马达满足如下方程组:
\[K_4 = \left\lbrace\begin{matrix*}[l] \ddot{y_1} + \dot{y_1} + 0.2(\dot{y_1}-\dot{y_2}) = \sin y_1 + \sin t \\ \ddot{y_2} + \dot{y_2} + 0.2(\dot{y_2}-\dot{y_1}) = \cos y_2 + \sin t \end{matrix*}\right\rbrace \] with initial condition:
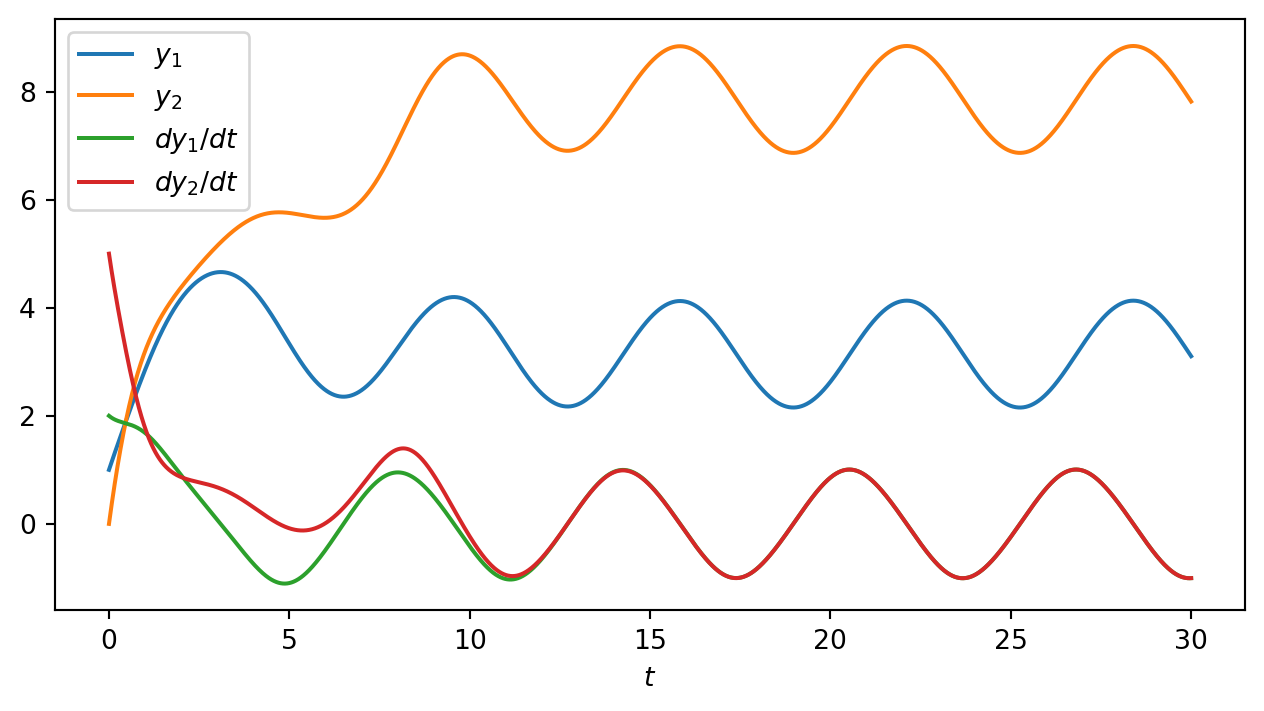
\[y_1(0) = 1; \dot{y}_1(0) = 2; ~~ y_2(0) = 0; ~~ \dot{y}_2(0) = 5\] 利用经典四阶Runge-Kutta法求解上述方程组,画出位移\(y_1,y_2\)和速率\(\dot{y}_1, \dot{y}_2\)随时间的演化关系图。
Solution 8.
%filename: chapter2_example_7_3_four_x_RK.m
function chapter3_example_7_3_four_x_RK
clear all
close all
clc
%四阶RK算法-----
a=0;x1 = 100; N = 1000;
h = (x1-a)/N;
t = a:h:x1;
y10=1; %初始条件
y20=0;
y30=2;
y40=5;
%--------------四阶RK算法------------------------
f=@(t,y)[y(3), y(4), -y(3)-0.2*(y(3)-y(4))+sin(y(1))+sin(t),-y(4)-0.2*(y(4)-y(3))+cos(y(2))+sin(t)]; % 定义 f,x(2)=p,x(1)=y
z0 = [y10,y20,y30,y40]; %初始条件
z = myrungekutta(f, t, z0);
yyy1 = z(:,1)'; %新版本的matlab可以不用转置,就可以画图。
yyy2 = z(:,2)';
yyy3 = z(:,3)';
yyy4 = z(:,4)';
figure;plot(t,yyy1,'b',t,yyy2,'r',t,yyy3,'k',t,yyy4,'g')
title('四阶常微分方程的数值解')
legend('Y1','Y2','dY1/dt','dY2/dt')
function z = myrungekutta(f, t, z0)
n = length(t);
h = t(2)-t(1);
%z=zeros(n,4);
z(1,:)=z0;
for i = 1:n-1
k1=f(t(i), z(i,:));
k2=f(t(i)+0.5*h, z(i,:) + h*k1/2);
k3=f(t(i)+0.5*h, z(i,:) + h*k2/2);
k4=f(t(i)+h, z(i,:) + h*k3);
z(i+1,:)=z(i,:) + h*(k1 + 2*k2 + 2*k3 + k4)/6;
end
Show the code
def ode(x, y):
res = y.copy()
y1 = res[0]
y2 = res[1]
z1 = res[2]
z2 = res[3]
y11 = z1
y22 = z2
z11 = -(z1 + 0.2 * (z1 - z2)) + np.sin(y1) + np.sin(x)
z22 = -(z2 + 0.2 * (z2 - z1)) + np.cos(y2) + np.sin(x)
return np.array([y11, y22, z11, z22])
def rk4(func, x0, y0, h, xp):
steps = int((xp - x0) / h)
result = np.zeros((steps + 1, len(y0)))
xis = np.zeros((steps + 1, 1))
xi = x0
yi = y0
xis[0] = x0
result[0, :] = yi
for i in range(steps):
k1 = func(xi, yi)
k2 = func(xi + 0.5 * h, yi + 0.5 * h * k1)
k3 = func(xi + 0.5 * h, yi + 0.5 * h * k2)
k4 = func(xi + h, yi + h * k3)
xi = xi + h
yi = yi + h / 6.0 * (k1 + 2.0 * k2 + 2.0 * k3 + k4)
xis[i + 1] = xi
result[i + 1, :] = yi
return xis, result
h = 0.01
x0 = 0
xp = 30.0
y0 = np.array([1.0, 0.0, 2.0, 5.0])
xi, yi = rk4(ode, x0, y0, h, xp)
plt.plot(xi, yi[:, 0], label = r'$y_1$')
plt.plot(xi, yi[:, 1], label = r'$y_2$')
plt.plot(xi, yi[:, 2], label = r'$dy_1/dt$')
plt.plot(xi, yi[:, 3], label = r'$dy_2/dt$')
plt.xlabel(r'$t$')
plt.legend()
plt.show()7 收敛性与稳定性
7.1 收敛性
若某算法对于任意固定的 \(x = x_i = x_0 + i h\),当 \(h\rightarrow0\) ( 同时 \(i\rightarrow \infty\)) 时有 \(y_i \rightarrow y(x_i)\),则称该算法是收敛的。 e.g.
\[\begin{eqnarray} \left\lbrace\begin{matrix*}[l] y' = \lambda y \\ y(0) = y_0 \end{matrix*}\right. \end{eqnarray}\]考察欧拉公式的收敛性。
sol:
该问题的精确解为 \(y(x) = y_0e^{\lambda x}\)
欧拉公式为 \(y_{i+1} = y_i + h\lambda y_i = (1+\lambda h) y_i \Rightarrow y_i = (1+\lambda h)^i y_0\)
对任意固定的 $x = x_i = i h $,有
\[y_i = y_0(1+\lambda h)^{x_i / h} = y_0[(1+\lambda h)^{1/\lambda h}]^{\lambda x_i} ~~~ \Rightarrow ~~~ y_0e^{\lambda x_i} = y(x_i)\]
\[\lim_{h\rightarrow 0} (1+\lambda h)^{1/\lambda h} = e.\]
7.2 稳定性
例8:考察初值问题 \(\begin{eqnarray} \left\lbrace\begin{matrix*}[l] y(x)' = -30y(x) \\ y(0) = 1 \end{matrix*}\right. \end{eqnarray}\) 在区间\([0, 0.5]\)上的解,分别用欧拉公式和改进的欧拉公式计算数值解(\(h=0.1\))。
%filename: chapter2_example_8_stable_Euler_tri.m
clear all
close all
clc
%比较Euler法、Euler法的梯形算法
h=0.06;%step %改变步长,考察稳定性
x1=[0:h:0.5];
N=(max(x1)-min(x1))/h;
y0=1; %the initial value
f=@(x,y)(-30*y);
%--------------解析解------------------------
y_e=exp(-30*x1);
%----------Euler算法------------------------------
y_euler=zeros(1,N+1);
y_euler(1)=y0;
for n=1:N %Euler法迭代公式
y_euler(n+1)=y_euler(n)-h*30*y_euler(n);
end
figure,subplot(2,1,1),plot(x1,y_e,'r',x1,y_euler,'-ob')
title('Euler法与精确结果比较图')
legend('精确解','Euler法结果')
subplot(2,1,2),plot(x1,abs(y_e-y_euler),'b')
title('Euler法与精确结果误差曲线')
y_euler
%--------------改进的Euler法,二阶RK算法----------------
y_2rk=zeros(1,N+1);
y_2rk(1)=y0;
for n=1:N
k1=f(x1(n),y_2rk(n));
k2=f(x1(n)+h,y_2rk(n)+h*k1);
y_2rk(n+1)=y_2rk(n)+h/2*(k1+k2);
end
figure,subplot(2,1,1),plot(x1,y_e,'r',x1,y_2rk,'-ob')
title('二阶RK算法与精确结果比较图')
legend('精确解','二阶RK算法结果')
subplot(2,1,2),plot(x1,abs(y_e-y_2rk),'b')
title('二阶RK算法与精确结果误差曲线')
y_2rk%filename: chapter2_example_8_stable_Euler_tri_RK.m
clear all
close all
clc
%比较Euler法、Euler法的梯形算法,四阶RK算法
h=0.09; %step %改变步长,考察稳定性
x1=[0:h:0.5];
N=(max(x1)-min(x1))/h;
y0=1; %the initial value
f=@(x,y)(-30*y);
%--------------解析解------------------------
y_e=exp(-30*x1);
%----------Euler算法------------------------------
y_euler=zeros(1,N+1);
y_euler(1)=y0;
for n=1:N %Euler法迭代公式
y_euler(n+1)=y_euler(n)-h*30*y_euler(n);
end
figure,subplot(2,1,1),plot(x1,y_e,'r',x1,y_euler,'-ob')
title('Euler法与精确结果比较图')
legend('精确解','Euler法结果')
subplot(2,1,2),plot(x1,abs(y_e-y_euler),'b')
title('Euler法与精确结果误差曲线')
y_euler
%--------------改进的Euler法,二阶RK算法----------------
y_2rk=zeros(1,N+1);
y_2rk(1)=y0;
for n=1:N
k1=f(x1(n),y_2rk(n));
k2=f(x1(n)+h,y_2rk(n)+h*k1);
y_2rk(n+1)=y_2rk(n)+h/2*(k1+k2);
end
figure,subplot(2,1,1),plot(x1,y_e,'r',x1,y_2rk,'-ob')
title('二阶RK算法与精确结果比较图')
legend('精确解','二阶RK算法结果')
subplot(2,1,2),plot(x1,abs(y_e-y_2rk),'b')
title('二阶RK算法与精确结果误差曲线')
y_2rk
%--------------RK算法------------------------
yy=zeros(1,N+1);
yy(1)=y0;
for n=1:N
k1=f(x1(n),yy(n));
k2=f(x1(n)+h/2,yy(n)+h/2*k1);
k3=f(x1(n)+h/2,yy(n)+h/2*k2);
k4=f(x1(n)+h,yy(n)+h*k3);
yy(n+1)=yy(n)+h/6*(k1+2*k2+2*k3+k4);
end
figure,subplot(2,1,1),plot(x1,y_e,'r',x1,yy,'b')
title('四阶RK算法与精确结果比较图')
legend('精确解','四阶RK算法结果')
subplot(2,1,2),plot(x1,abs(y_e-yy),'r')
title('四阶RK算法与精确结果间的误差')稳定性的另一个例子
Euler公式从向前差分公式获得,如果从其他差分形式出发,以对称差分(中心差分)近似 \(f' \approx \frac{f_{+1} - f_{-1}}{2h}\) 来逼近 \(y' = f (x, y)\)中的导数,可得到由三项构成的一个递推关系(二阶方法) \[y_{n+1} = y_{n-1} + 2hf(x_n, y_n)+O(h^3)\] –> 多步法
e.g. \[\begin{eqnarray} \left\lbrace\begin{matrix*}[l] y(x)' = -y(x) \\ y(0) = 1 \end{matrix*}\right. \end{eqnarray}\], 其精确解为 \(y = e^{-x}\),取步长 \(h=0.2\) or \(0.1\), \(y_0 = 1, y_n = ?\), \[\begin{eqnarray} y_1 = \left\lbrace\begin{matrix*}[l] e^{-h} \\ 1-h+\frac{1}{2}h^2 + O(h^3) \end{matrix*}\right. \end{eqnarray}\]
sol:
%filename: chapter2_example_9_stable.m
% example9 稳定性
clear all
close all
clc
x_in=10; %要求点的自变量值
y=@(x)exp(-x); %精确值
x=0:0.001:x_in;
h=0.01;
x0=0;
m=(x_in-x0)/h;
yy=zeros(1,m+1); %存储Euler法结果
yyy=zeros(1,m+1);%存储中心差分法结果
xx=x0:h:x_in;
%-----------%Euler method--------------
yy(1)=1;
for n=1:m %Euler method
yy(n+1)=yy(n)-h*yy(n);
end
%----------利用中心差分公式推导出的Euler法-----------
yyy(1)=1;
yyy(2)=exp(-h); %尝试改成exp(-h)
for n=2:m
yyy(n+1)=yyy(n-1)-2*h*yyy(n);
end
hold on
plot(x,y(x),'r',xx,yy,'k',xx,yyy,'b-o')
legend('精确解','Euler法','中心差分')
hold offDefinition 1 若某算法在计算过程中任一步产生的误差在以后的计算中都逐步衰减,则称该算法是绝对稳定的。
一般分析时为简单起见,只考虑试验方程 \[y' = \lambda y\]
对于给定步长\(h>0\),在计算 \(y_n\) 时引入了误差\(r_n\) ,若这个误差在计算后面的\(y_{n+i} (i=1,2,…)\) 中所引起的误差按绝对值均不增加,就说该数值方法对于这个步长 \(h\) 和\(\lambda\) 常数是绝对稳定的。为保证方法的绝对稳定,步长 \(h\) 和\(\lambda\) 就有其相应的允许范围,称其为该方法的
以Euler方法为例 \(y_{n+1} = y_n + \lambda h y_n\)
误差方程 \(\rho_{n+1} = \rho_n(1+\lambda h) ~~~ \rho_{n+1}/\rho_n=1+\lambda h\)
绝对稳定区域 \(|1+\lambda h| \leq 1\)
对于例8中的存在的误差增大现象,\(\lambda = -30\)
绝对稳定区域为 \(|1-30h|\leq 1 ~~~ \Rightarrow ~~~ 0\leq h \leq 1/15\)
\(h=0.1\)显然不在其绝对稳定区域内,可尝试\(h=0.05\)
在例9中,当我们使用中心差分推得的递推公式时,
\[y_{n+1} = y_{n-1} -2hy_n\]
误差方程为 \(\rho_{n+1} = \rho_{n-1} - 2h\rho_n ~~~~ \frac{\rho_{n+1}}{\rho_n} - \frac{\rho_{n-1}}{\rho_n} = -2h\)
let \(K_n = \frac{\rho_n}{\rho_{n-1}} ~~~ \Rightarrow ~~~ K_{n+1}-\frac{1}{K_{n}} = -2h\)
\(K_{n+1}\sim K_n ~~~~~ K_n^2 + 2hK_n - 1 = 0\)
\[K_n = -h \pm \sqrt{1+h^2}\]
\[\left| -h\pm\sqrt{1+h^2} \right| \leq 1\]
由此,不论 \(h\) 取多少,都不能保证绝对稳定。
\[\rho_{n+1} = \left[ 1+(h\lambda) + \frac{(h\lambda)^2}{2!} + \frac{(h\lambda)^3}{3!} + \frac{(h\lambda)^4}{4!} \right]\rho_n\]
\[\Rightarrow \left| 1+(h\lambda) + \frac{(h\lambda)^2}{2!} + \frac{(h\lambda)^3}{3!} + \frac{(h\lambda)^4}{4!} \right| \leq 1\]
\[-2.78 < \lambda h < 0\]
%filename: chapter2_example_8_RK.m
%求解例题8中的实验函数的绝对稳定区间,针对经典四阶RK算法
%从图形可以看出,0.1也不在绝对稳定区域内
clear all
close all
clc
h=0:0.0001:0.12;
a=-30;
y=1+a*h+(a*h).^2/2+(a*h).^3/6+(a*h).^4/24;
plot(h,y,'r',h,1,'b',h,-1,'b')%filename: chapter2_example_8_stable_Euler_tri_RK.m
clear all
close all
clc
%比较Euler法、Euler法的梯形算法,四阶RK算法
h=0.09; %step %改变步长,考察稳定性
x1=[0:h:0.5];
N=(max(x1)-min(x1))/h;
y0=1; %the initial value
f=@(x,y)(-30*y);
%--------------解析解------------------------
y_e=exp(-30*x1);
%----------Euler算法------------------------------
y_euler=zeros(1,N+1);
y_euler(1)=y0;
for n=1:N %Euler法迭代公式
y_euler(n+1)=y_euler(n)-h*30*y_euler(n);
end
figure,subplot(2,1,1),plot(x1,y_e,'r',x1,y_euler,'-ob')
title('Euler法与精确结果比较图')
legend('精确解','Euler法结果')
subplot(2,1,2),plot(x1,abs(y_e-y_euler),'b')
title('Euler法与精确结果误差曲线')
y_euler
%--------------改进的Euler法,二阶RK算法----------------
y_2rk=zeros(1,N+1);
y_2rk(1)=y0;
for n=1:N
k1=f(x1(n),y_2rk(n));
k2=f(x1(n)+h,y_2rk(n)+h*k1);
y_2rk(n+1)=y_2rk(n)+h/2*(k1+k2);
end
figure,subplot(2,1,1),plot(x1,y_e,'r',x1,y_2rk,'-ob')
title('二阶RK算法与精确结果比较图')
legend('精确解','二阶RK算法结果')
subplot(2,1,2),plot(x1,abs(y_e-y_2rk),'b')
title('二阶RK算法与精确结果误差曲线')
y_2rk
%--------------RK算法------------------------
yy=zeros(1,N+1);
yy(1)=y0;
for n=1:N
k1=f(x1(n),yy(n));
k2=f(x1(n)+h/2,yy(n)+h/2*k1);
k3=f(x1(n)+h/2,yy(n)+h/2*k2);
k4=f(x1(n)+h,yy(n)+h*k3);
yy(n+1)=yy(n)+h/6*(k1+2*k2+2*k3+k4);
end
figure,subplot(2,1,1),plot(x1,y_e,'r',x1,yy,'b')
title('四阶RK算法与精确结果比较图')
legend('精确解','四阶RK算法结果')
subplot(2,1,2),plot(x1,abs(y_e-yy),'r')
title('四阶RK算法与精确结果间的误差')8 Matlab commands
ode45解非刚性微分方程,中等精度,使用Runge-Kutta法的四、五阶算法。ode23解非刚性微分方程,低精度,使用Runge-Kutta法的二、三阶算法。ode113解非刚性微分方程,Adams-Bashforth-Moulton PECE法。ode23t解中等的刚性微分方程,使用自由内插法的梯形法则。ode15s解刚性微分方程,使用可变阶次的数值微分(NDFs)算法。ode23s解刚性微分方程,低阶方法,使用修正的Rosenbrock公式。ode23tb解刚性微分方程,低阶方法,使用TR-BDF2方法.
注:常微分方程分为“刚性的”和“非刚性的”。刚性的是指其Jacobian矩阵的特征值相差十分悬殊。二者对步长选择的要求不同。
ode45的使用步骤:
- 编写计算导数的M函数文件,该函数的输出量是“一阶导数向量Y’ ”,输入量是自变量和函数量Y;函数体描述一阶方程组右边的表达式。
- 给定解方程的条件与要求
- 调用指令求解并处理结果
ode45命令使用的语句格式如下:(其余指令用法类似)
[T,Y]=ode45(odefun,tspan,y0,options),其中
odefun为要求解的常微分方程的函数句柄; tspan为单调递增或递减的积分区间,如\([1, 8]\); y0为初始条件矢量,其中矢量元素的排列顺序要求与函数中的元素顺序一致;
options为用odeset建立的优化选项,可以略去采用默认选项 T是输出的时间列矢量,矩阵Y的每个列矢量是解的一个分量。
Show the code
\[y{\left(x \right)} = \sqrt{2 x + 1}\]
%filename: chapter2_example_6_Matlab.m
function jyjs
clear all
close all
clc
options=odeset('RelTol',1e-12);
[X,Y]=ode45(@yjs,[0,1],1,options); %[0,1]为自变量取值范围,1为初始条件
yy=@(xx)sqrt(1+2*xx);%解析结果
subplot(2,1,1);plot(X',Y','r',X',yy(X'),'b')
subplot(2,1,2);plot(X',Y'-yy(X'),'r')
%定义句柄函数
function ydot=yjs(x,y)
ydot=y-2*x/y;scipy.integrate.odeint(func, y0, t, args=(), Dfun=None,
col_deriv=0, full_output=0, ml=None, mu=None, rtol=None,
atol=None, tcrit=None, h0=0.0, hmax=0.0, hmin=0.0, ixpr=0,
mxstep=0, mxhnil=0, mxordn=12, mxords=5, printmessg=0,
tfirst=False)[source]\[y' = p; ~~~ p' = -4\pi^2y\]
%filename: chapter2_example_7_erbianliang_Matlab.m
function jyjs_2
clear
clc
close all
format long
options=odeset('RelTol',1e-13);
[X,Y]=ode45(@yjs,[0,10],[5;0],options);
%--------------解析解------------------------
y0=5; %初始位置,可以任意设置
p0=0; %初始动量,可以任意设置
m=1; %谐振子的质量为1
k=4*pi^2; %弹簧的劲度系数
A=sqrt(y0^2+p0^2/(m*k)); %谐振子的振幅
pha=acos(y0/A); %谐振子的初始相位,若x0与p0同号,pha为负,否则pha为正
t=X';
y_e=A*cos(sqrt(k/m)*t+pha); %谐振子的精确解
p_e=-m*A*sqrt(k/m)*sin(sqrt(k/m)*t+pha); %动量的精确解
E_e=p_e.^2/(2*m)+0.5*k*y_e.^2 %能量的精确值
E_m=Y(:,2)'.^2/(2*m)+0.5*k*Y(:,1)'.^2; %能量的数值解
figure;
subplot(2,2,1);plot(X,Y(:,1),'r',X,y_e,'b')
subplot(2,2,2);plot(X,Y(:,2),'r',X,p_e,'b')
subplot(2,2,3);plot(Y(:,1),Y(:,2))
subplot(2,2,4);plot(X',E_m-E_e,'r')
%定义句柄函数
function ydot=yjs(t,y)
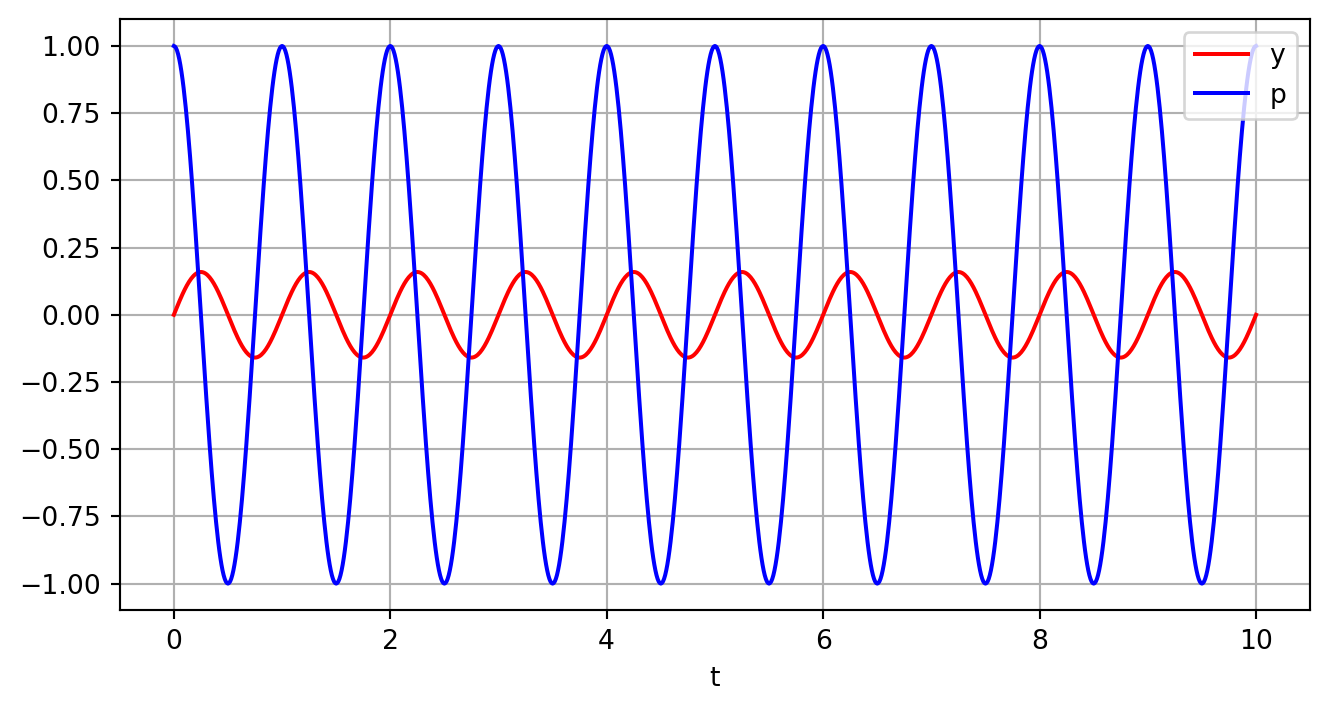
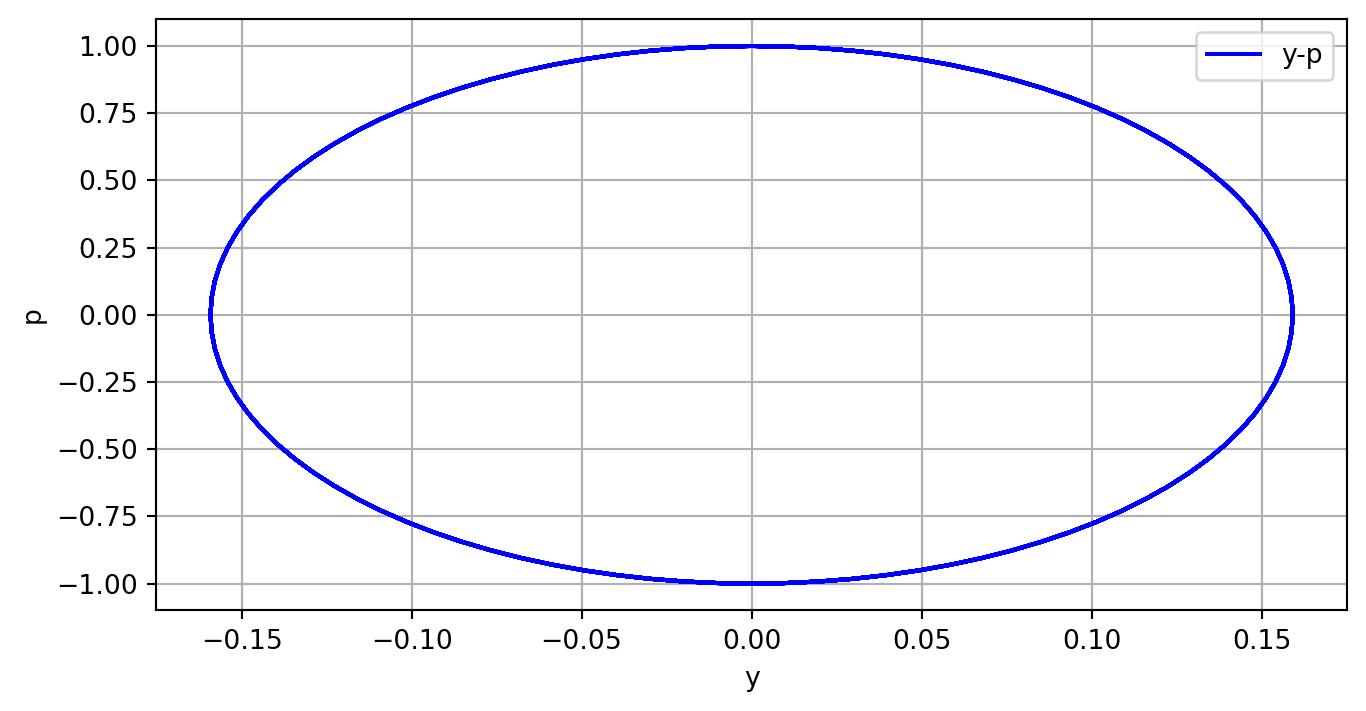
ydot=[y(2);-4*pi^2*y(1)];Show the code
def func(y, t):
return [y[1], -4*np.pi**2*y[0]]
y0 = [0, 1]
t = np.linspace(0, 10, 1001)
sol = scipy.integrate.odeint(func, y0, t)
plt.figure()
plt.plot(t, sol[:, 0], 'r', label='y')
plt.plot(t, sol[:, 1], 'b', label='p')
plt.legend(loc='best')
plt.xlabel('t')
plt.grid()
plt.show()
plt.figure()
plt.plot(sol[:, 0], sol[:, 1], 'b', label='y-p')
plt.legend(loc='best')
plt.xlabel('y')
plt.ylabel('p')
plt.grid()
plt.show()\[y = -\frac{x^3}{6} - \frac{x^2}{2} + 2.5x + 6e^{x-1} + \frac{1}{6}\]
Show the code
\[y{\left(x \right)} = - \frac{x^{3}}{6} - \frac{x^{2}}{2} + \frac{5 x}{2} + \frac{6 e^{x}}{e} + \frac{1}{6}\]
%filename: chapter2_example_7_2_sanbianliang_Matlab.m
function jyjs
clear
clc
close all
format long
options=odeset('RelTol',1e-14);
[X,Y]=ode45(@yjs,[1,6],[8;7;4],options); %[1,6]为自变量取值范围,[8,7,4]为初始条件
yy=@(x)(5*x)/2+(6*exp(x))/exp(1)-x.^2/2-x.^3/6 +1/6;%解析结果
subplot(2,1,1);plot(X,Y(:,1),'r',X,yy(X),'b')
title('三阶常微分方程的数值解与解析解')
subplot(2,1,2);plot(X,Y(:,1)-yy(X),'r')
title('三阶常微分方程的数值解的误差')
%定义句柄函数
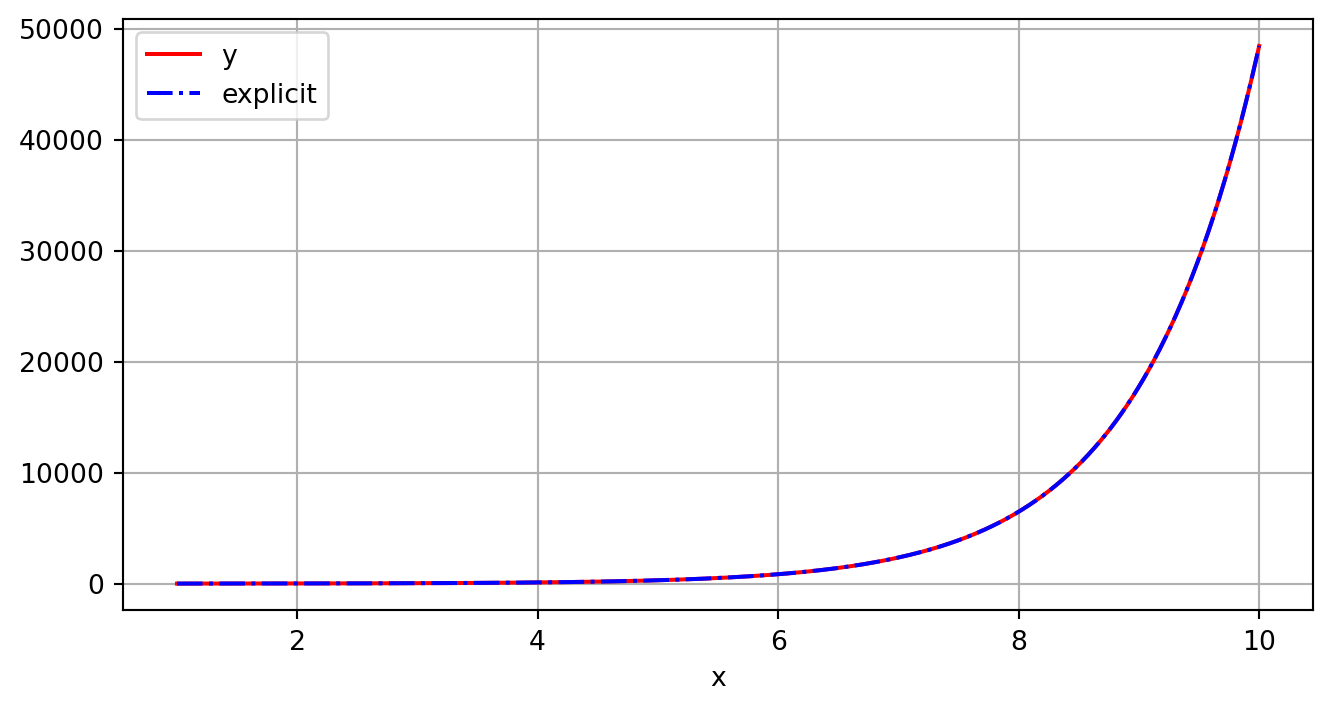
function ydot=yjs(xx,y)
ydot=[y(2);y(3);y(3)+xx];Show the code
def func(y, t):
return [y[1], y[2], y[2] + t]
y0 = [8, 7, 4]
x0 = 1
t = np.linspace(1, 10, 1001)
sol = scipy.integrate.odeint(func, y0, t)
plt.figure()
plt.plot(t, sol[:, 0], 'r', label='y')
callfct = lambdify((x), res.rhs)
plt.plot(t, callfct(t), 'b-.', label = 'explicit')
plt.legend(loc='best')
plt.xlabel('x')
plt.grid()
plt.show()9 Seminar: Chaos in dynamics
Show the code
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.cm as cm
# Parameters
x_res, y_res = 300, 300
xmin, xmax = -1.5, 1.5
width = xmax - xmin
ymin, ymax = -1.5, 1.5
height = ymax - ymin
z_abs_max = 10
max_iter = 1000
def julia_set(c):
# Initialise an empty array (corresponding to pixels)
julia = np.zeros((x_res, y_res))
# Loop over each pixel
for ix in range(x_res):
for iy in range(y_res):
# Map pixel position to a point in the complex plane
z = complex(ix / x_res * width + xmin,
iy / y_res * height + ymin)
# Iterate
iteration = 0
while abs(z) <= z_abs_max and iteration < max_iter:
z = z**2 + c
iteration += 1
iteration_ratio = iteration / max_iter
# Set the pixel value to be equal to the iteration_ratio
julia[ix, iy] = iteration_ratio
# Plot the array using matplotlib's imshow
fig, ax = plt.subplots()
ax.imshow(julia, interpolation='nearest', cmap=cm.gnuplot2)
plt.axis('off')
plt.show()
c = -0.1-0.65j
julia_set(c)一根长度为 \(l\) 的钟摆被限制在一垂直的平面内,在强迫外力 \(f_d\) 和阻力 \(f_r\) 的作用下振荡运动。钟摆的运动可以通过 Newton 方程来描述 \[ ma = f_g + f_d + f_r \] 其中 \(f_g = -mg \sin \theta\) 是重力在运动方向的分力,\(a=l d^2\theta/dt^2\) 是沿切线方向的加速度, \(\theta\) 是杆和垂线的夹角。
假设强迫外力为 \(f = f_d^0 \cos \omega_0 t\)
阻力为 \(f_r = -kv = -kl \frac{d\theta}{dt}\).
那么 Newton 运动方程就可以写成如下形式
\[ \frac{d^2\theta}{dt^2} + q\frac{d\theta}{dt} + \sin\theta = b \cos\omega_0 t \] 其中 \(q = \frac{k}{m}, b = \frac{f_d^0}{ml}\)
并且取 \((l/g)^{1/2}\) 为时间单位。
let \(x_1 = \theta, x_2 = \frac{d\theta}{dt}\)
\(\Rightarrow\)
\[\begin{eqnarray} \left\lbrace\begin{matrix*}[l] \frac{dx_1}{dt} = x_2 \\ \frac{dx_2}{dt} = -qx_2 - \sin x_1 + b \cos \omega_0 t \end{matrix*}\right. \end{eqnarray}\]function dirven_pendulum
clear all
close all
clc
q=0.5;
b=1.9;
omega0=2/3; %周期性强迫外力的频率
theta0=pi*160/180; %初始角度,以弧度为单位
time = 1000; N = 160000;
h = time/N;
t = 0:h:time;
f=@(t,x)[x(2), -q*x(2)-sin(x(1))+b*cos(omega0*t)];%定义句柄函数
z0 = [theta0, 0]; %初始条件,注意角度采用弧度单位,角速度为0
z = myrungekutta(f, t, z0);
theta = z(:,1);
omega = z(:,2);
subplot(2,1,1)
plot(t, theta,'b',t,omega,'r')
title('驱动单摆的角度与角速度随时间的变化关系')
legend('角度','角速度')
subplot(2,1,2)
plot(theta, omega)
%plot(theta(N/2:N), omega(N/2: N))
title('角度-角速度相图')
figure;
subplot(2,1,1),plot(t,theta','b',t,theta0*cos(t),'r')
title('角度演化的数值与解析比较')
legend('数值结果','解析结果')
subplot(2,1,2),plot(t,theta'-theta0*cos(t),'r')
function z = myrungekutta(f, t, z0)
n = length(t);
h = t(2)-t(1);
z(1,:)=z0;
for i = 1:n-1
k1=f(t(i), z(i,:));
k2=f(t(i)+0.5*h, z(i,:) + h*k1/2);
k3=f(t(i)+0.5*h, z(i,:) + h*k2/2);
k4=f(t(i)+h, z(i,:) + h*k3);
z(i+1,:)=z(i,:) + h*(k1 + 2*k2 + 2*k3 + k4)/6;
end
Show the code
q = 0.5
b = 1.9
omega = 2/3.0
theta0 = np.pi * 160 / 180
y0 = np.array([theta0, 0])
t_end = 1000
steps = 160000
h = t_end / steps
def ode(x, y):
x1 = y[0]
x2 = y[1]
res = np.array([x2, -q * x2 - np.sin(x1) + b * np.cos(omega * x)])
return res
xi, yi = rk4(ode, 0, y0, h, t_end)
plt.plot(xi, yi[:, 0])
plt.plot(xi, yi[:, 1])
plt.show()function dirven_pendulum
clear all
close all
clc
q=0;
b=0;
omega0=2/3; %周期性强迫外力的频率
theta0=pi*3/180; %初始角度3度,以弧度为单位
time = 50; N = 20000;
h = time/N;
t = 0:h:time;
f=@(t,x)[x(2), -q*x(2)-sin(x(1))+b*cos(omega0*t)];%定义句柄函数
z0 = [theta0, 0]; %初始条件,注意角度采用弧度单位,角速度为0
z = myrungekutta(f, t, z0);
theta = z(:,1);
omega = z(:,2);
subplot(2,1,1)
plot(t, theta,'b',t,omega,'r')
title('驱动单摆的角度与角速度随时间的变化关系')
legend('角度','角速度')
subplot(2,1,2)
plot(theta, omega)
%plot(theta(N/2:N), omega(N/2: N))
title('角度-角速度相图')
figure;
subplot(2,1,1),plot(t,theta','b',t,theta0*cos(t),'r')
title('角度演化的数值与解析比较')
legend('数值结果','解析结果')
subplot(2,1,2),plot(t,theta'-theta0*cos(t),'r')
function z = myrungekutta(f, t, z0)
n = length(t);
h = t(2)-t(1);
z(1,:)=z0;
for i = 1:n-1
k1=f(t(i), z(i,:));
k2=f(t(i)+0.5*h, z(i,:) + h*k1/2);
k3=f(t(i)+0.5*h, z(i,:) + h*k2/2);
k4=f(t(i)+h, z(i,:) + h*k3);
z(i+1,:)=z(i,:) + h*(k1 + 2*k2 + 2*k3 + k4)/6;
end
Show the code
q = 0
b = 0
omega = 2/3.0
theta0 = np.pi * 3 / 180
y0 = np.array([theta0, 0])
t_end = 50
steps = 20000
h = t_end / steps
xi, yi = rk4(ode, 0, y0, h, t_end)
plt.subplot(121)
plt.plot(xi, yi[:, 0], label = r'$\theta$')
plt.plot(xi, yi[:, 1], label = r'$\dot{\theta}$')
plt.xlabel(r'$t$')
plt.legend()
plt.subplot(122)
plt.plot(yi[:, 0], yi[:, 1], label = r'$\theta-\dot{\theta}$')
plt.xlabel(r'$\theta$')
#plt.ylabel(r'$\dot{\theta}$')
plt.legend()
plt.show()Show the code
from sympy.solvers.ode.systems import dsolve_system
var('t q omega b')
var('x1 x2', cls = Function)
eqn1 = Eq(x1(t).diff(t), x2(t))
eqn2 = Eq(x2(t).diff(t), -q * x2(t) - x1(t) + b * cos(omega * t))
ics = {x1(0): theta0, x2(0): 0}
results = dsolve_system([eqn1, eqn2], [x1(t), x2(t)], ics = ics)
Markdown(f'$${latex(results)}$$')\[\left[ \left[ x_{1}{\left(t \right)} = - \frac{b \left(q - \sqrt{q^{2} - 4}\right) \left(q + \sqrt{q^{2} - 4}\right) e^{- \frac{t \left(q + \sqrt{q^{2} - 4}\right)}{2}} \int e^{\frac{t \left(q + \sqrt{q^{2} - 4}\right)}{2}} \cos{\left(\omega t \right)}\, dt}{4 \sqrt{q^{2} - 4}} + \frac{b \left(q - \sqrt{q^{2} - 4}\right) \left(q + \sqrt{q^{2} - 4}\right) e^{- \frac{t \left(q - \sqrt{q^{2} - 4}\right)}{2}} \int e^{\frac{t \left(q - \sqrt{q^{2} - 4}\right)}{2}} \cos{\left(\omega t \right)}\, dt}{4 \sqrt{q^{2} - 4}} - \frac{b \left(5.0 \cdot 10^{15} q^{4} - q^{3} \left(1.0 \cdot 10^{16} \sqrt{0.25 q^{2} - 1} + 5.0 \cdot 10^{15} \sqrt{q^{2} - 4}\right) + q^{2} \left(1.0 \cdot 10^{16} \sqrt{0.25 q^{2} - 1} \sqrt{q^{2} - 4} - 2.0 \cdot 10^{16}\right) + 2.0 \cdot 10^{16} q \left(\sqrt{0.25 q^{2} - 1} + \sqrt{q^{2} - 4}\right) - 2.0 \cdot 10^{16} \sqrt{0.25 q^{2} - 1} \sqrt{q^{2} - 4}\right) \int\limits^{0} e^{0.5 q t} e^{1.0 t \sqrt{0.25 q^{2} - 1}} \cos{\left(\omega t \right)}\, dt - 261799387799150.0 q^{5} + q^{4} \left(523598775598299.0 \sqrt{0.25 q^{2} - 1} + 261799387799150.0 \sqrt{q^{2} - 4}\right) - q^{3} \left(523598775598299.0 \sqrt{0.25 q^{2} - 1} \sqrt{q^{2} - 4} - 1.30899693899575 \cdot 10^{15}\right) - q^{2} \left(1.5707963267949 \cdot 10^{15} \sqrt{0.25 q^{2} - 1} + 1.30899693899575 \cdot 10^{15} \sqrt{q^{2} - 4}\right) + q \left(1.5707963267949 \cdot 10^{15} \sqrt{0.25 q^{2} - 1} \sqrt{q^{2} - 4} - 1.0471975511966 \cdot 10^{15}\right) + 1.0471975511966 \cdot 10^{15} \sqrt{q^{2} - 4}}{1.0 \cdot 10^{16} q^{5} e^{\frac{t \left(q + \sqrt{q^{2} - 4}\right)}{2}} - 2.0 \cdot 10^{16} q^{4} \left(0.25 q^{2} - 1\right)^{0.5} e^{\frac{t \left(q + \sqrt{q^{2} - 4}\right)}{2}} - 7.0 \cdot 10^{16} q^{3} e^{\frac{t \left(q + \sqrt{q^{2} - 4}\right)}{2}} + 1.0 \cdot 10^{17} q^{2} \left(0.25 q^{2} - 1\right)^{0.5} e^{\frac{t \left(q + \sqrt{q^{2} - 4}\right)}{2}} + 1.2 \cdot 10^{17} q e^{\frac{t \left(q + \sqrt{q^{2} - 4}\right)}{2}} - 8.0 \cdot 10^{16} \left(0.25 q^{2} - 1\right)^{0.5} e^{\frac{t \left(q + \sqrt{q^{2} - 4}\right)}{2}}} + \frac{\left(b \left(- 5.0 \cdot 10^{15} q^{3} + q^{2} \left(1.0 \cdot 10^{16} \sqrt{0.25 q^{2} - 1} - 5.0 \cdot 10^{15} \sqrt{q^{2} - 4}\right) + 1.0 \cdot 10^{16} q \left(\sqrt{0.25 q^{2} - 1} \sqrt{q^{2} - 4} + 1\right) + 1.0 \cdot 10^{16} \sqrt{q^{2} - 4}\right) \int\limits^{0} e^{0.5 q t} e^{- 1.0 t \sqrt{0.25 q^{2} - 1}} \cos{\left(\omega t \right)}\, dt + 261799387799150.0 q^{2} - q \left(523598775598299.0 \sqrt{0.25 q^{2} - 1} - 261799387799150.0 \sqrt{q^{2} - 4}\right) - 523598775598299.0 \sqrt{0.25 q^{2} - 1} \sqrt{q^{2} - 4}\right) e^{- \frac{t \left(q - \sqrt{q^{2} - 4}\right)}{2}}}{- 1.0 \cdot 10^{16} q^{2} + 2.0 \cdot 10^{16} q \left(0.25 q^{2} - 1\right)^{0.5} + 4.0 \cdot 10^{16}}, \ x_{2}{\left(t \right)} = - \frac{b \left(q - \sqrt{q^{2} - 4}\right) e^{- \frac{t \left(q - \sqrt{q^{2} - 4}\right)}{2}} \int e^{\frac{t \left(q - \sqrt{q^{2} - 4}\right)}{2}} \cos{\left(\omega t \right)}\, dt}{2 \sqrt{q^{2} - 4}} + \frac{b \left(q + \sqrt{q^{2} - 4}\right) e^{- \frac{t \left(q + \sqrt{q^{2} - 4}\right)}{2}} \int e^{\frac{t \left(q + \sqrt{q^{2} - 4}\right)}{2}} \cos{\left(\omega t \right)}\, dt}{2 \sqrt{q^{2} - 4}} + \frac{b \left(1.0 \cdot 10^{16} q^{3} - 2.0 \cdot 10^{16} q^{2} \sqrt{0.25 q^{2} - 1} - 4.0 \cdot 10^{16} q + 4.0 \cdot 10^{16} \sqrt{0.25 q^{2} - 1}\right) \int\limits^{0} e^{0.5 q t} e^{1.0 t \sqrt{0.25 q^{2} - 1}} \cos{\left(\omega t \right)}\, dt - 523598775598299.0 q^{4} + 1.0471975511966 \cdot 10^{15} q^{3} \sqrt{0.25 q^{2} - 1} + 2.6179938779915 \cdot 10^{15} q^{2} - 3.14159265358979 \cdot 10^{15} q \sqrt{0.25 q^{2} - 1} - 2.0943951023932 \cdot 10^{15}}{1.0 \cdot 10^{16} q^{5} e^{\frac{t \left(q + \sqrt{q^{2} - 4}\right)}{2}} - 2.0 \cdot 10^{16} q^{4} \left(0.25 q^{2} - 1\right)^{0.5} e^{\frac{t \left(q + \sqrt{q^{2} - 4}\right)}{2}} - 7.0 \cdot 10^{16} q^{3} e^{\frac{t \left(q + \sqrt{q^{2} - 4}\right)}{2}} + 1.0 \cdot 10^{17} q^{2} \left(0.25 q^{2} - 1\right)^{0.5} e^{\frac{t \left(q + \sqrt{q^{2} - 4}\right)}{2}} + 1.2 \cdot 10^{17} q e^{\frac{t \left(q + \sqrt{q^{2} - 4}\right)}{2}} - 8.0 \cdot 10^{16} \left(0.25 q^{2} - 1\right)^{0.5} e^{\frac{t \left(q + \sqrt{q^{2} - 4}\right)}{2}}} - \frac{\left(b \left(- 1.0 \cdot 10^{16} q^{2} + 2.0 \cdot 10^{16} q \sqrt{0.25 q^{2} - 1} + 2.0 \cdot 10^{16}\right) \int\limits^{0} e^{0.5 q t} e^{- 1.0 t \sqrt{0.25 q^{2} - 1}} \cos{\left(\omega t \right)}\, dt + 523598775598299.0 q - 1.0471975511966 \cdot 10^{15} \sqrt{0.25 q^{2} - 1}\right) e^{- \frac{t \left(q - \sqrt{q^{2} - 4}\right)}{2}}}{- 1.0 \cdot 10^{16} q^{2} + 2.0 \cdot 10^{16} q \left(0.25 q^{2} - 1\right)^{0.5} + 4.0 \cdot 10^{16}}\right]\right]\]
\(\displaystyle x_{1}{\left(t \right)} = 0.0261799387799149 e^{i t} + 0.0261799387799149 e^{- i t}\)
\(\displaystyle x_{2}{\left(t \right)} = 0.0261799387799149 i e^{i t} - 0.0261799387799149 i e^{- i t}\)
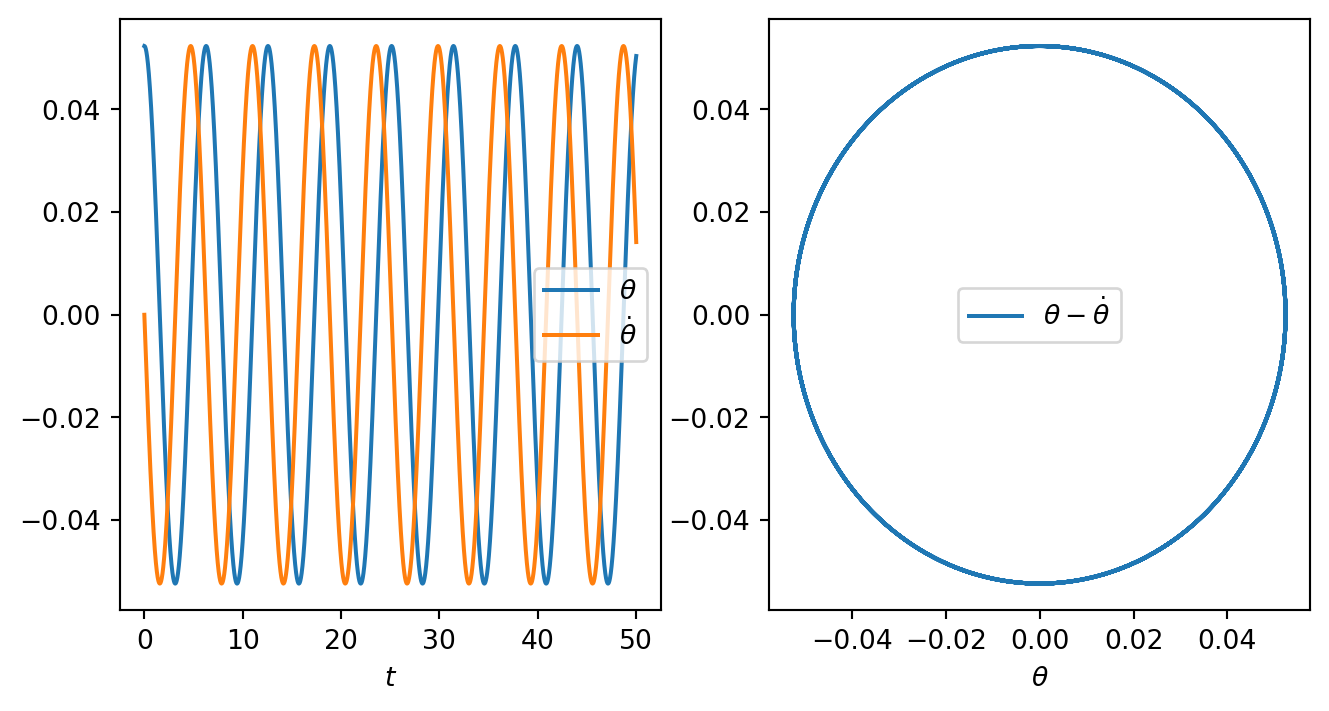
Show the code
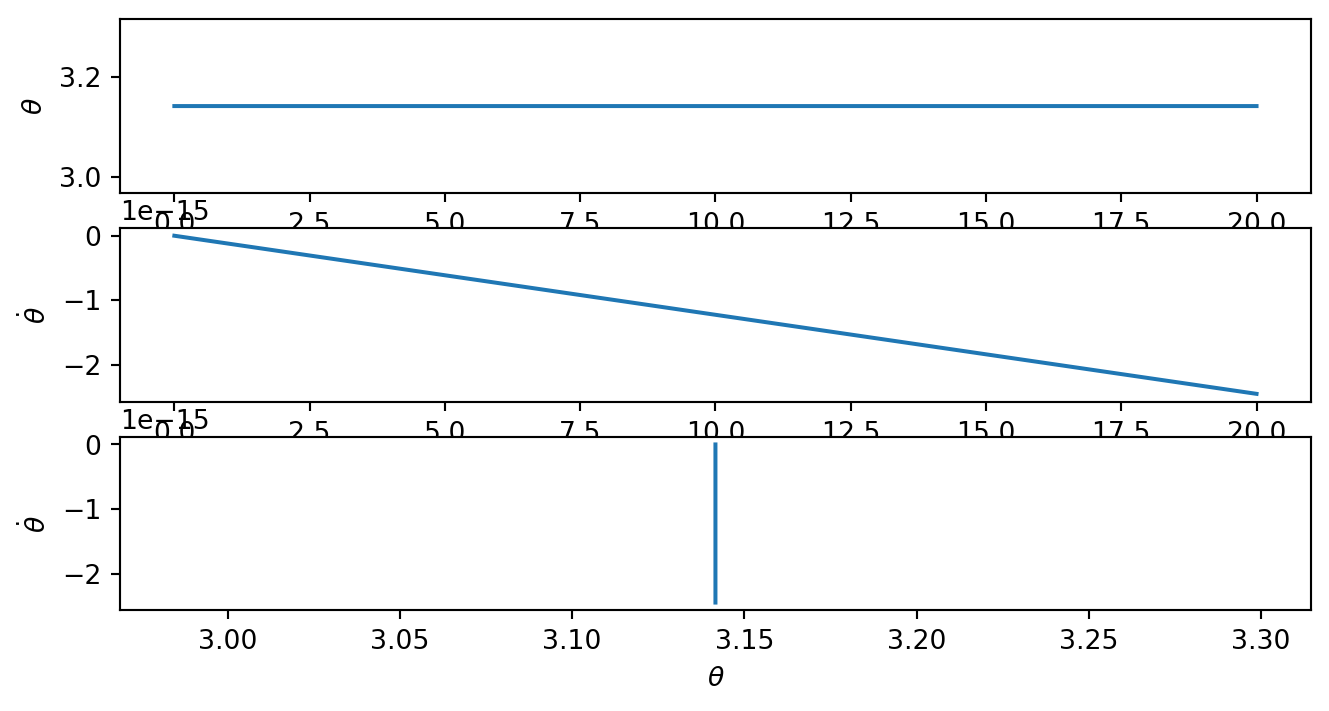
\(q=0,b=0, t=50\),初始角度小于\(5^\circ\)。即无阻尼,小角度释放的情况,钟摆运动是一个简谐运动, i.e., \(\theta(t) = \theta_0 \cos \omega t\).
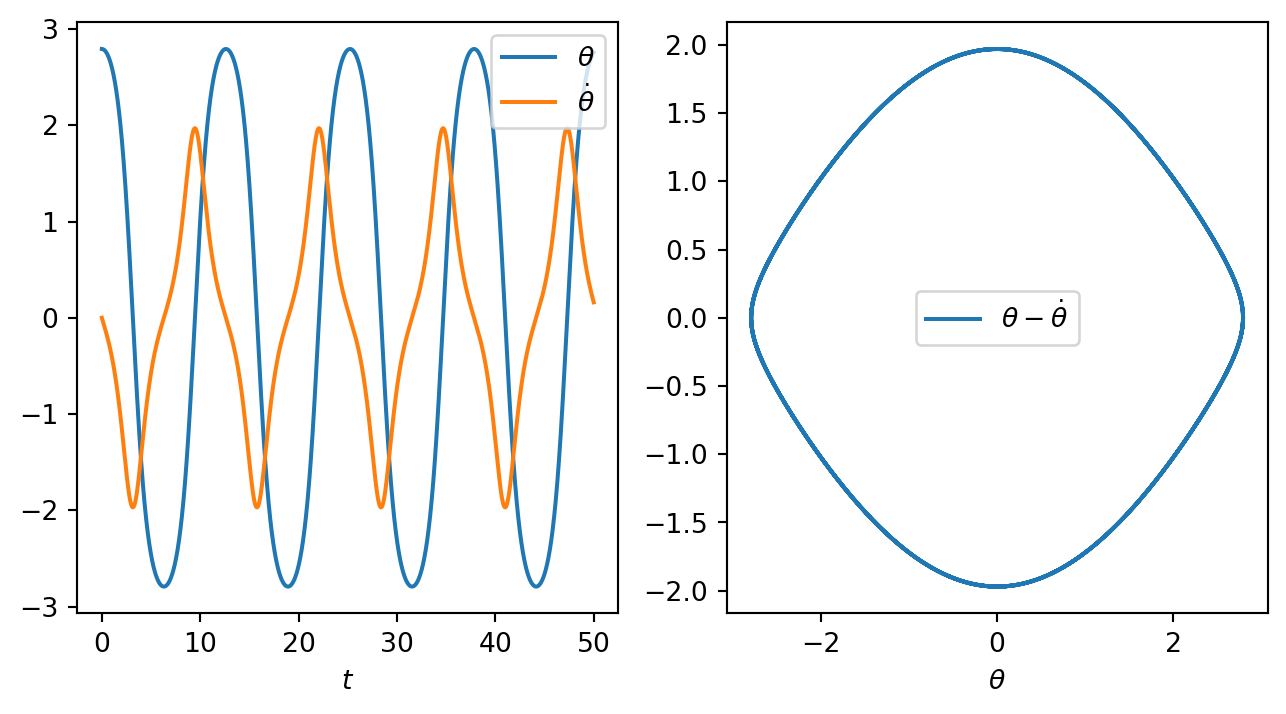
\(q=0,b=0, t=50\),初始角度为\(160^\circ\)。即无驱动,无阻尼,大角度释放的情况。
显然钟摆运动不再是简谐运动,但仍是周期运动。
%filename: DrivenPendulum_case2.m
function dirven_pendulum
clear all
close all
clc
q=0;
b=0;
omega0=2/3; %周期性强迫外力的频率
theta0=pi*100/180; %初始角度160度,以弧度为单位
time = 50; N = 20000;
h = time/N;
t = 0:h:time;
f=@(t,x)[x(2), -q*x(2)-sin(x(1))+b*cos(omega0*t)];%定义句柄函数
z0 = [theta0, 0]; %初始条件,注意角度采用弧度单位,角速度为0
z = myrungekutta(f, t, z0);
theta = z(:,1);
omega = z(:,2);
subplot(2,1,1)
plot(t, theta,'b',t,omega,'r')
title('驱动单摆的角度与角速度随时间的变化关系')
legend('角度','角速度')
subplot(2,1,2)
plot(theta, omega)
%plot(theta(N/2:N), omega(N/2: N))
title('角度-角速度相图')
function z = myrungekutta(f, t, z0)
n = length(t);
h = t(2)-t(1);
z(1,:)=z0;
for i = 1:n-1
k1=f(t(i), z(i,:));
k2=f(t(i)+0.5*h, z(i,:) + h*k1/2);
k3=f(t(i)+0.5*h, z(i,:) + h*k2/2);
k4=f(t(i)+h, z(i,:) + h*k3);
z(i+1,:)=z(i,:) + h*(k1 + 2*k2 + 2*k3 + k4)/6;
end
Show the code
q = 0
b = 0
omega = 2/3.0
theta0 = np.pi * 160 / 180
y0 = np.array([theta0, 0])
t_end = 50
steps = 20000
h = t_end / steps
xi, yi = rk4(ode, 0, y0, h, t_end)
plt.subplot(121)
plt.plot(xi, yi[:, 0], label = r'$\theta$')
plt.plot(xi, yi[:, 1], label = r'$\dot{\theta}$')
plt.xlabel(r'$t$')
plt.legend()
plt.subplot(122)
plt.plot(yi[:, 0], yi[:, 1], label = r'$\theta-\dot{\theta}$')
plt.xlabel(r'$\theta$')
#plt.ylabel(r'$\dot{\theta}$')
plt.legend()
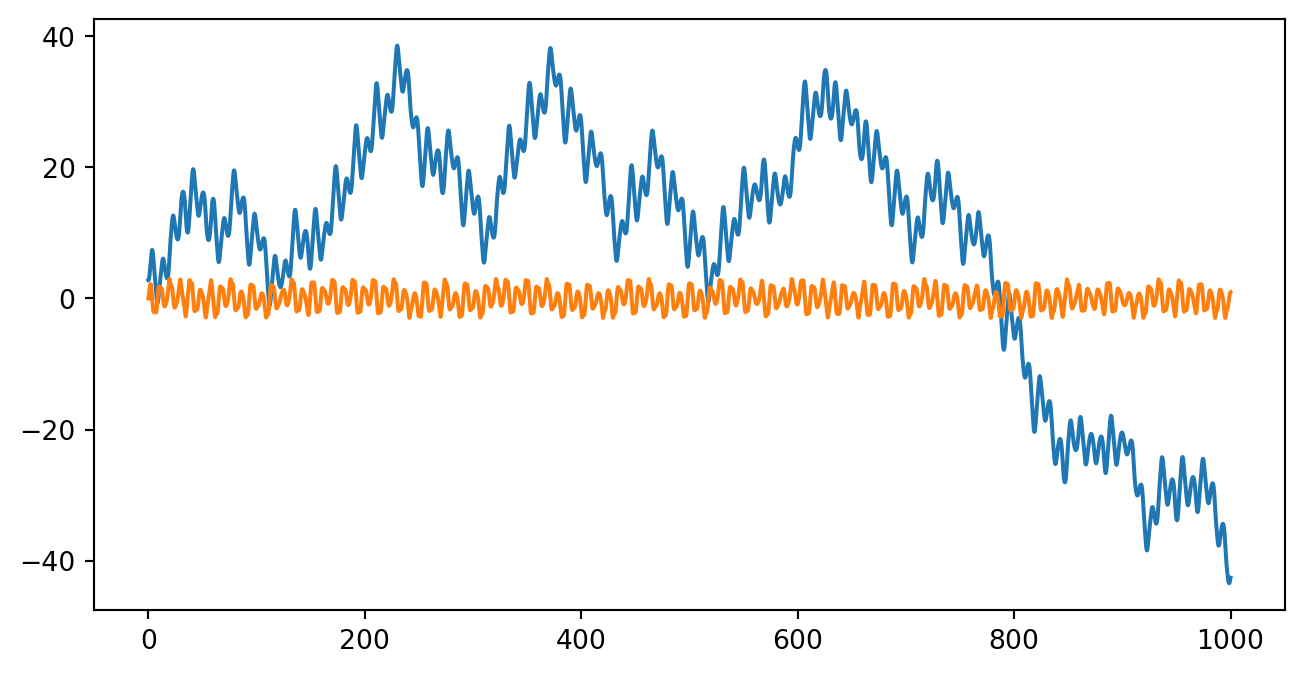
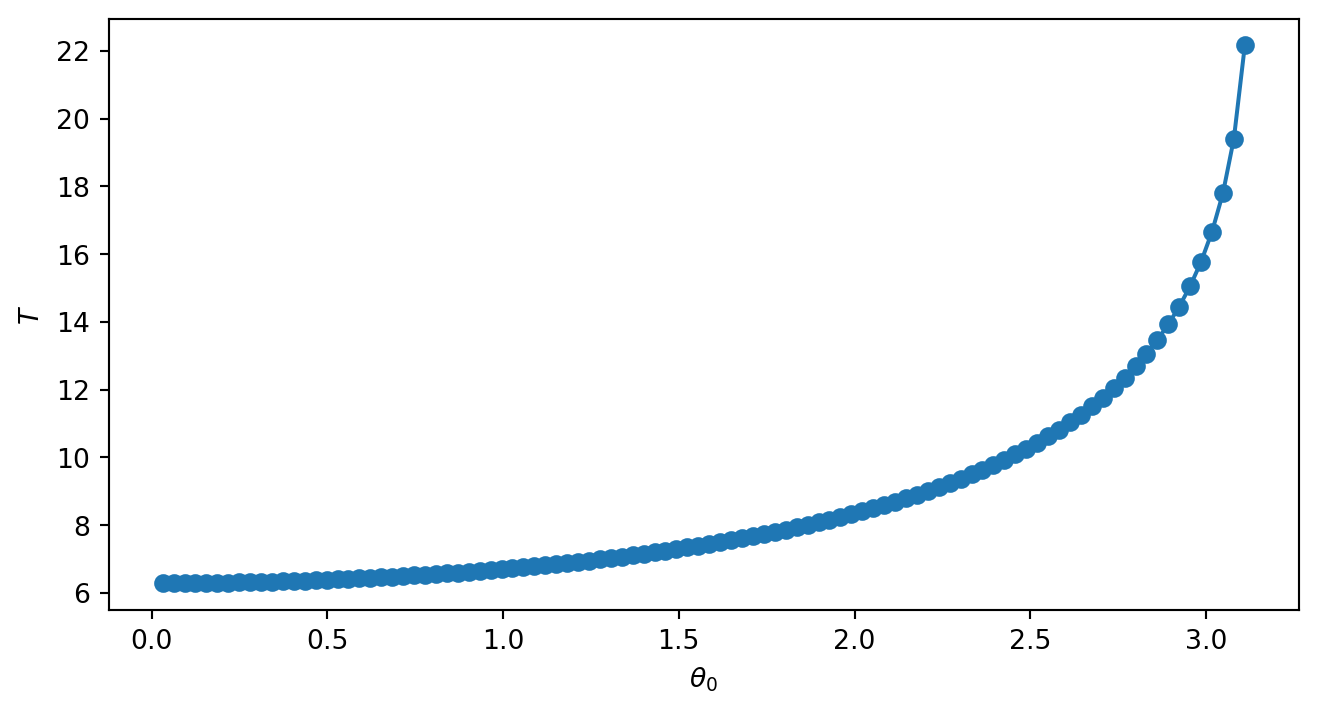
plt.show()9.0.1 初始角度与周期的关系如何?
%filename: dirven_pendulum_duration.m
function dirven_pendulum
clear all
close all
clc
q=0;
b=0;
w0=2/3; %周期性强迫外力的频率
theta0=linspace(pi/360,pi-pi/360,30); %初始角度,以弧度为单位
omega0=0; %自由释放,角速度为0
time = 20; N = 50000;
h = time/N;
t = 0:h:time;
f=@(t,x)[x(2), -q*x(2)-sin(x(1))+b*cos(w0*t)];
%定义句柄函数
for i=1:length(theta0)
z0 = [theta0(i), omega0]; %初始条件,注意角度采用弧度单位,角速度为0
z = myrungekutta(f, t, z0);
theta = z(:,1)';
omega = z(:,2)';
for j=1:N-1
if omega(j+1)*omega(j)<0 %符号相反表示钟摆开始改变运动方向
%该程序的缺点是RK算法会计算所有时间,不论钟摆完成多少个周期运动
TT(i)=(2*j+1)*h
break; %跳出当前所在for循环
end
end
end
plot(theta0,TT,'o-');
title('驱动单摆的初始角度与周期的关系')
xlabel('初始角度'); ylabel('周期');
function z = myrungekutta(f, t, z)
n = length(t);
h = t(2)-t(1);
for i = 1:n-1
k1=f(t(i), z(i,:));
k2=f(t(i)+0.5*h, z(i,:) + h*k1/2);
k3=f(t(i)+0.5*h, z(i,:) + h*k2/2);
k4=f(t(i)+h, z(i,:) + h*k3);
z(i+1,:)=z(i,:) + h*(k1 + 2*k2 + 2*k3 + k4)/6;
end
%filename: dirven_pendulum_duration2.m
function duration
clear;
clc
theta=linspace(pi/360,350*pi/360,300);
T=[];
options=odeset('Events',@events);%开启事件判断功能
%解不同的初始角度下的周期值
for i=1:length(theta)
[t,u]=ode45(@f,[0,50],[theta(i),0],options);
T=[T,2*t(end)];
end
hold on
plot(theta,T,'r*-')
title('周期与摆角的关系');
xlabel('摆角'); ylabel('周期');
function ydot=f(t,y)
q=0;
b=0;
w0=2/3; %周期性强迫外力的频率
ydot=[y(2);-q*y(2)-sin(y(1))+b*cos(w0*t)];
function [value,isterminal,direction]=events(t,y)
value=y(2); %监控的值为角速度
isterminal=1; %isterminal=1表示中断运算
direction=1;%direction=1表示由负变到零Show the code
q = 0
b = 0
omega = 2/3.0
t_end = 50
steps = 20000
h = t_end / steps
theta0s = np.linspace(0.01, 0.99, 100) * np.pi
dur = np.zeros(theta0s.shape)
for i in range(len(theta0s)):
theta0 = theta0s[i]
y0 = np.array([theta0, 0])
xi, yi = rk4(ode, 0, y0, h, t_end)
mytheta = yi[:, 0]
mythetam = mytheta[0:-1]
mythetap = mytheta[1:]
indexes = np.where(mythetam < mythetap)
#print(i, indexes)
dur[i] = 2 * xi[indexes[0][0]]
plt.plot(theta0s, dur, '-o')
plt.xlabel(r'$\theta_0$')
plt.ylabel(r'$T$')
plt.show()/var/folders/r_/ctnsy93118b_yw2h5rqqpmxh0000gn/T/ipykernel_3078/880524029.py:19: DeprecationWarning:
Conversion of an array with ndim > 0 to a scalar is deprecated, and will error in future. Ensure you extract a single element from your array before performing this operation. (Deprecated NumPy 1.25.)
9.0.2 当初始摆角为180o时,单摆的运动如何?
%filename: DrivenPendulum_case3.m
function dirven_pendulum
clear all
close all
clc
q=0;
b=0;
omega0=2/3; %周期性强迫外力的频率
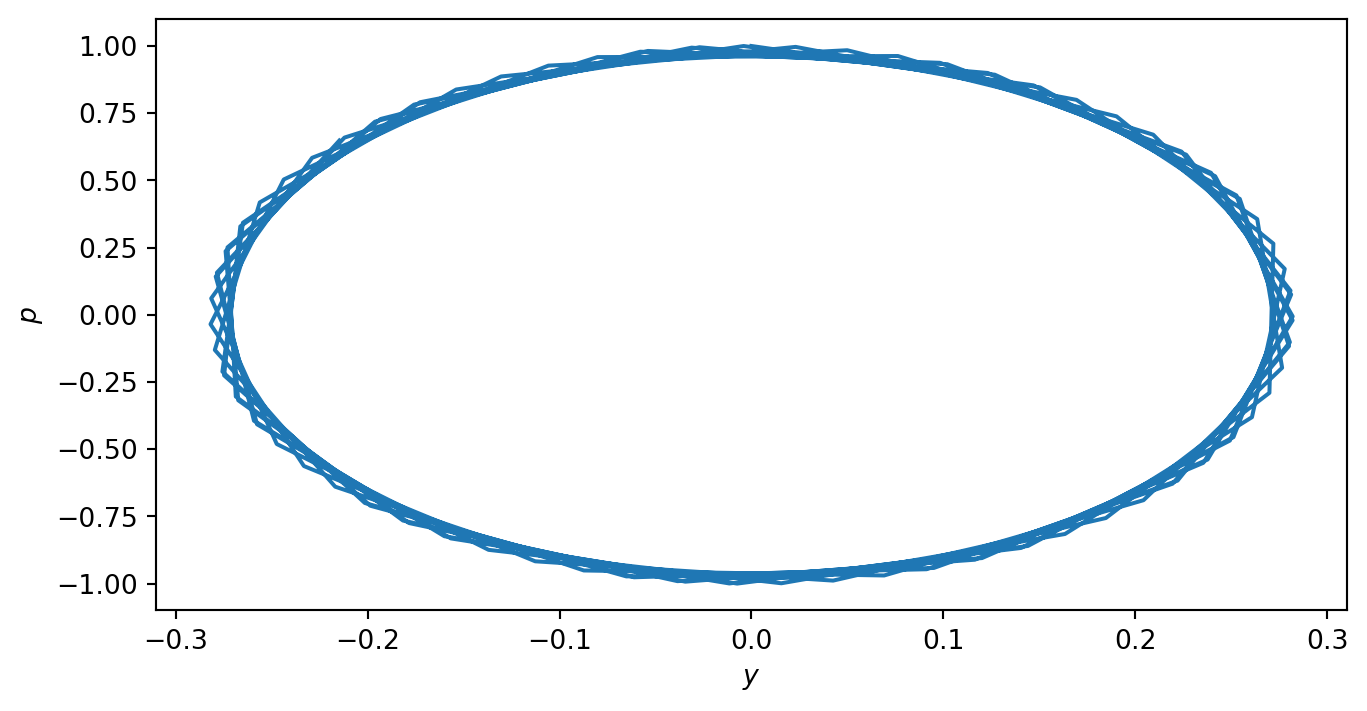
theta0=pi; %初始角度为180度,以弧度为单位
time = 20; N = 80000;
h = time/N;
t = 0:h:time;
f=@(t,x)[x(2), -q*x(2)-sin(x(1))+b*cos(omega0*t)];%定义句柄函数
z = [theta0, 1]; %初始条件,注意角度采用弧度单位,角速度为1
z = myrungekutta(f, t, z);
theta = z(:,1);
omega = z(:,2);
subplot(3,1,1)
plot(t, theta,'b')%,t,omega,'r')
title('驱动单摆的角度随时间的变化关系')
subplot(3,1,2)
plot(t, omega,'b')%,t,omega,'r')
title('驱动单摆的角速度随时间的变化关系')
%title('驱动单摆的角度与角速度随时间的变化关系')
%legend('角度','角速度')
subplot(3,1,3)
plot(theta, omega)
%plot(theta(N/2:N), omega(N/2: N))
title('角度-角速度相图')
function z = myrungekutta(f, t, z)
n = length(t);
h = t(2)-t(1);
for i = 1:n-1
k1=f(t(i), z(i,:));
k2=f(t(i)+0.5*h, z(i,:) + h*k1/2);
k3=f(t(i)+0.5*h, z(i,:) + h*k2/2);
k4=f(t(i)+h, z(i,:) + h*k3);
z(i+1,:)=z(i,:) + h*(k1 + 2*k2 + 2*k3 + k4)/6;
end
Show the code
q = 0
b = 0
omega = 2/3.0
theta0 = np.pi * 180 / 180
y0 = np.array([theta0, 0])
t_end = 20
steps = 80000
h = t_end / steps
xi, yi = rk4(ode, 0, y0, h, t_end)
plt.subplot(311)
plt.plot(xi, yi[:, 0], label = r'$\theta$')
plt.xlabel(r'$t$')
plt.ylabel(r'$\theta$')
plt.subplot(312)
plt.plot(xi, yi[:, 1], label = r'$\dot{\theta}$')
plt.xlabel(r'$t$')
plt.ylabel(r'$\dot{\theta}$')
plt.subplot(313)
plt.plot(yi[:, 0], yi[:, 1], label = r'$\theta-\dot{\theta}$')
plt.xlabel(r'$\theta$')
plt.ylabel(r'$\dot{\theta}$')
plt.show()单摆做旋转运动,由初速度决定运动状态
10 
11 
12 
13 
14 
15 
16 
17 
18 
19 Seminar 2: 阻尼斜抛运动的数值求解
研究受空气阻力作用的斜抛运动。设抛体质量为\(m\),初速度为\(v_0\),受空气阻力的大小\(R\)与速度\(v\)的\(n\)次方成正比,即\(R=bvn\),其中\(b\)是阻尼系数。
将抛体视为质点,根据牛顿运动定律,抛体的运动微分方程可以写为
\[ m\frac{d^2\vec{r}}{dt^2} = -m\vec{g} - bv^n \frac{\vec{v}}{v} = -m\vec{g} - bv^{n-1}\vec{v} \]
以抛出点为原点建立直角坐标系,\(Ox\)沿水平方向,\(Oy\)沿垂直向上。则上述运动方程可以化为
\[\begin{eqnarray} \left\lbrace \begin{matrix*}[l] \frac{d^2x}{dt^2} = -\frac{b}{m}(v_x^2 + v_y^2)^{\frac{n-1}{2}}v_x \\ \frac{d^2y}{dt^2} = -g -\frac{b}{m}(v_x^2 + v_y^2)^{\frac{n-1}{2}}v_y \end{matrix*} \right. \end{eqnarray}\]对上述方程组进行降阶,令 \[y_1 = x;~~ y_2 = \dot{x} = v_x; ~~ y_3 = y;~~ y_4 = v_y\] 可得:
\[\begin{eqnarray} \left\lbrace \begin{matrix*}[l] \frac{dy_1}{dt} = y_2; ~~ \frac{dy_2}{dt} = -\frac{b}{m}(y_2^2 + y_4^2)^{\frac{n-1}{2}}y_2 \\ \frac{dy_3}{dt} = y_4; ~~ \frac{dy_4}{dt} = -g -\frac{b}{m}(y_2^2 + y_4^2)^{\frac{n-1}{2}}y_4 \\ \end{matrix*} \right. \end{eqnarray}\]令初始条件为: \[y_1 =0;~y_2 = \dot{x} = 30;~y_3 = 0;~y_4=\dot{y} = 50\] 求以下情况中抛体的运动轨迹:
- \(b=0\),即没有阻尼的情形;
- 有阻尼,\(n=1\)的情形;
- 有阻尼,\(n=2\)的情形;