Chapt 3: BVP & EVP of ODE

Author
Affiliation

Feng Wan

B832@仲英楼 or 3133@泓理楼 // School of Physcis @ Xian Jiaoton University

Show the code 
import numpy as np
import matplotlib.pyplot as plt
from sympy import *

1 边值问题与本征值问题介绍

2 Classification of ODE

IVP

给定待求函数在某个初始点上的值

\[\begin{eqnarray} \left\lbrace\begin{matrix*} \frac{dy}{dx} = f(x, y) \\ y|_{x = a} = y_0 \end{matrix*}\right. \end{eqnarray}\]
BVP

在自变量的两个端点上对待求函数施加约束，如函数值约束、导数值约束…

\[\begin{eqnarray} \left\lbrace\begin{matrix*} y''+\frac{\pi^2}{4}y+\frac{\pi^2}{4} = 0 \\ y(0) = 0, y(1) = 1 \end{matrix*}\right. \end{eqnarray}\]
EVP

一类特殊的含有参数的边值问题。只有在参数取特定值时，方程才有非零解

\[\begin{eqnarray} \left\lbrace\begin{matrix*} \frac{d^2\varphi(x)}{dx^2} + k^2\varphi(x) = 0 \\ \varphi(0) = \varphi(1) = 0 \end{matrix*}\right. \end{eqnarray}\]
BVP

在区间的两个端点上对待求函数各施加一个约束，这样方程的解就能唯一的确定

\[\Rightarrow ~~~ y(x) = \cos\frac{\pi}{2}x +2\sin\frac{\pi}{2}x-1\]

EVP

在区间的两个端点上对待求函数各施加一个约束。方程存在一个待定参数，只有当待定参数取特定值时，方程才存在非零解

\[\Rightarrow k_n = n\pi;~~\phi_n \sim \sin n\pi~~(n=1,2,...)\]

2.1 物理学中边值问题和本征值问题的一般形式

物理学中许多重要的微分方程可写成线性二阶微分方程的形式

\[ \frac{d^2y}{dx^2} + \underbrace{k^2(x)}_{\text{Real function}}y = \underbrace{S(x)}_{\text{source term}} \]

当\(k^2>0\) 时，齐次方程 (\(S = 0\))的解是振荡的，其局部波数为\(k\)；当\(k^2<0\)时，齐次方程的解是指数增长或衰减的，局部变化率为 \((-k^2)^{1/2}\).

2.1.1 边值问题的例子——泊松方程

考虑求解一个定域的电荷分布\(r(r)\)所产生的静电势\(\Phi\)

Poisson 方程为 \(\nabla^2 \Phi = -4\pi\rho\)

对于这个方程，我们通常关心的是在\(r = 0\)和\(r = + \infty\)上满足某种约束条件的解（如势能在\(r = 0\)和\(r = + \infty\)处都为\(0\)），这个问题就是一个边值问题．

\[ \nabla^2\Phi = \frac{1}{r^2}\partial_r (r^2 \partial_r \Phi) + \frac{1}{r^2\sin\theta} \partial_\theta (\sin\theta \partial_\theta \Phi) + \frac{1}{r^2\sin\theta}\partial^2_\phi \Phi \]

\[ \nabla^2 \Phi = -4\pi\rho ~~~ \xrightarrow{\text{for spherical symmetrical }r\text{ and }\Phi} ~~~ \frac{1}{r^2}\frac{d}{dr}\left[r^2\frac{d\Phi}{dr}\right] \]

substitute \(\Phi(r) = r^{-1}\phi(r) \longrightarrow \frac{d^2\phi}{dr^2} = -4\pi r \rho\)

i.e. \(\frac{d^2y}{dx^2} + k^2(x)y = S(x) \longrightarrow k^2 = 0, ~~ S = -4\pi r \rho\).

If \(\rho(r) = \frac{1}{8\pi}e^{-r} \longrightarrow \frac{d^2\phi}{dr^2} = -\frac{1}{2}re^{-r} \longrightarrow \phi(r) = 1 - \frac{1}{2}(r+2)e^{-r}\).

Show the code 
from IPython.display import Markdown
from sympy.solvers.ode.systems import dsolve_system
from sympy import *
var('r')
var('phi', cls = Function)

eqn = Eq(phi(r).diff(r, 2), -1/2*r*exp(-r))
Markdown(f'$${latex(eqn)}$$')

\[\frac{d^{2}}{d r^{2}} \phi{\left(r \right)} = - 0.5 r e^{- r}\]

Show the code 
res = dsolve([eqn], [phi(r)], ics = {phi(0): 0, phi(oo): 0})
Markdown(f'$${latex(res[0])}$$')

\[\phi{\left(r \right)} = - 0.5 r e^{- r} + 1 - 1.0 e^{- r}\]

2.2 本征值问题的例子——薛定谔方程

量子力学中，一个质量为\(m\)，能量为\(E\)的粒子在中心位势\(V(r)\)中运动，其波函数满足如下的薛定谔方程 \[ \left[-\frac{\hbar^2}{2m}\nabla^2 + V(r)\right]\Psi = E\Psi \] \(\longrightarrow\) \[ \Psi(r, \theta, \phi) = r^{-1}R(r)Y_{lm}(\theta, \phi) \]

\[ -\frac{\hbar^2}{2m}\left[ \frac{1}{r^2}\partial_r (r^2 \partial_r) + \frac{1}{r^2\sin\theta} \partial_\theta (\sin\theta \partial_\theta) + \frac{1}{r^2\sin\theta}\partial^2_\phi \right] = (E-V(r))\Psi \]

Radial wavefunction \(R\): \(\frac{d^2R}{dr^2} + \underbrace{\frac{2m}{\hbar} \left[ E - \frac{l(l+1)\hbar^2}{2mr^2} - V(r) \right]}_{k^2(r)}R = \underbrace{0}_{S = 0} \leftrightarrow \frac{d^2y}{dx^2} + k^2(x)y = S(x)\)

对于该方程，我们感兴趣的是对哪些能量本征值\(E\)，能够导出满足适当边界条件的物理上可以接受的非零解，这个问题就是一个本征值问题。

对于上述两类问题：

  1. 物理情况所施加的边界条件，常常是以在自变量的两个单独的点上对因变量的约束的形式出现，不能作为初值问题求解。
  2. 对于本征方程，首先必须求出本征值。

针对常微分方程 \(\frac{d^2y}{dx^2} + k^2(x)y = S(x)\) 的一种特别有效的算法。

二阶导数的3点差分公式 \(f''(x_0) = \frac{f(x_0 + h) - 2f(x_0) + f(x_0 - h)}{h^2} + O(h^2)\)

首先用二阶导数的3点差分公式 \(f'' = \frac{f_{+1} - 2f_0 + f_{-1}}{h^2}\) 以及方程 \[\frac{d^2y}{dx^2} + k^2(x)y = S(x)\]

求解y的四阶导数:

\[\begin{eqnarray} y_n'''' &=& \frac{d^2}{dx^2}(-k^2y + S)|_{x = x_n } \\ &=& -\frac{(k^2y)_{n+1} - 2(k^2y)_n + (k^2y)_{n-1}}{h^2} + \frac{S_{n+1} - 2S_n + S_{n-1}}{h^2} + O(h^2) \end{eqnarray}\]

\[ f_{\pm 1} \equiv f(\pm h) = f_0 \pm hf' + \frac{h^2}{2}f'' \pm \frac{h^3}{6}f''' + \frac{h^4}{24}f^{(4)} \pm \frac{h^5}{5!}f^{(5)} + O(h^6) \]

\[ f_{+1} + f_{-1} = 2f_0 + h^2f'' + \frac{h^4}{12}f^{(4)} + O(h^6) \]

\[ \Rightarrow \frac{f_{+1} - 2f_0 + f_{-1}}{h^2} = f'' + \frac{h^2}{12}f^{(4)} + O(h^4) \]

\[ \Rightarrow \frac{y_{n+1} -2y_n + y_{n-1}}{h^2} = y'' + \frac{h^2}{12}y_n^{(4)} + O(h^4) \]

\[\begin{eqnarray} \Rightarrow \frac{y_{n+1} -2y_n + y_{n-1}}{h^2} = (S_n - k_n^2 y_n) &-& \frac{k^2_{n+1} y_{n+1} - 2k_n^2y_n + k^2_{n-1}y_{n-1}}{12} \\ &+& \frac{S_{n+1} - 2S_n + S_{n-1}}{12} + O(h^4) \end{eqnarray}\]
Numerove method

按照\(y\)的同类项整理可得

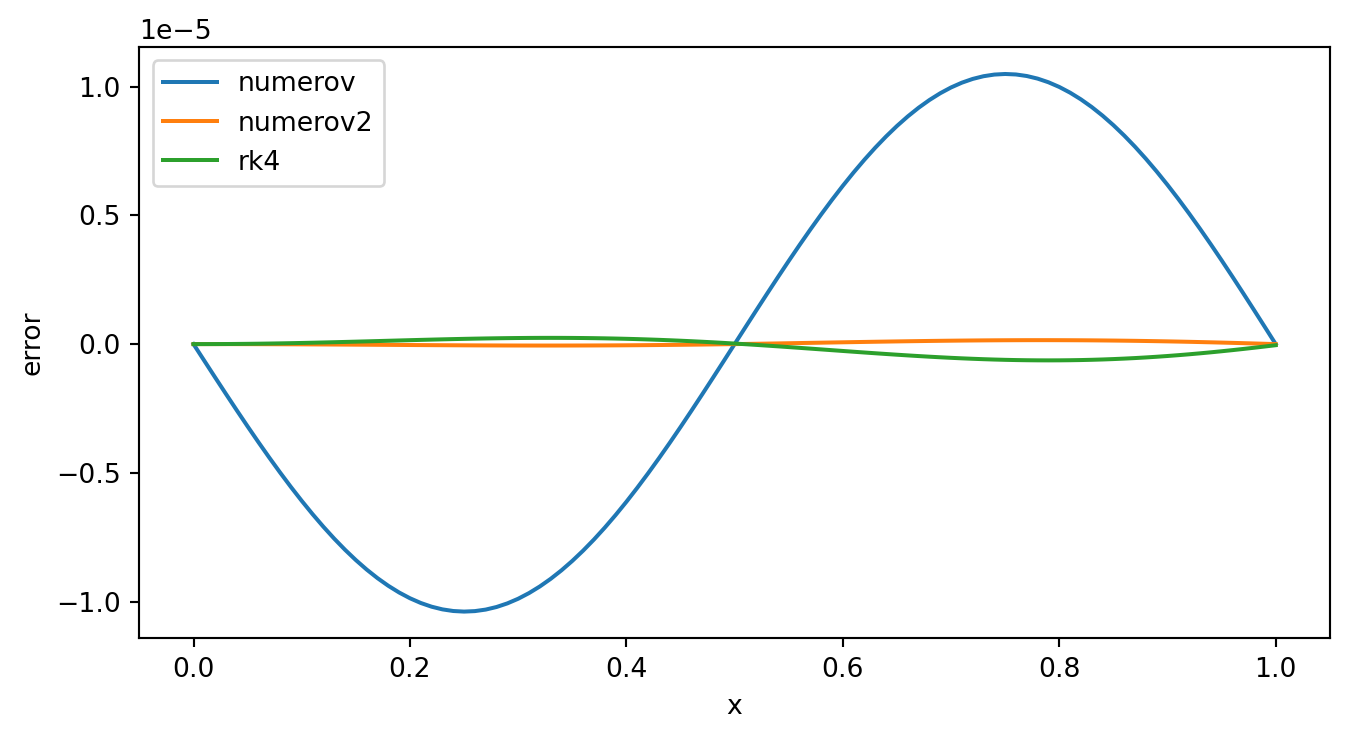
\[\begin{eqnarray} \left( 1 + \frac{h^2}{12}k_{n+1}^2 \right)y_{n+1} - 2\left( 1 - \frac{5h^2}{12}k_n^2 \right)y_n &+& \left( 1 + \frac{h^2}{12}k_{n-1}^2 \right)y_{n-1} \\ &=& \frac{h^2}{12}(S_{n+1} + 10S_n + S_{n-1}) + O(h^6) \end{eqnarray}\]

这是一个关于\(y_{n+1}\) 或者 \(y_{n-1}\) 的线性方程。对 \(y_{n+1}\) 或者 \(y_{n-1}\) 解此线性方程，就提供了一个对 \(x\) 向前或向后的递推关系，其局部截断误差为 \(O(h^6)\)，其精度比四阶RK方法还要高一阶。

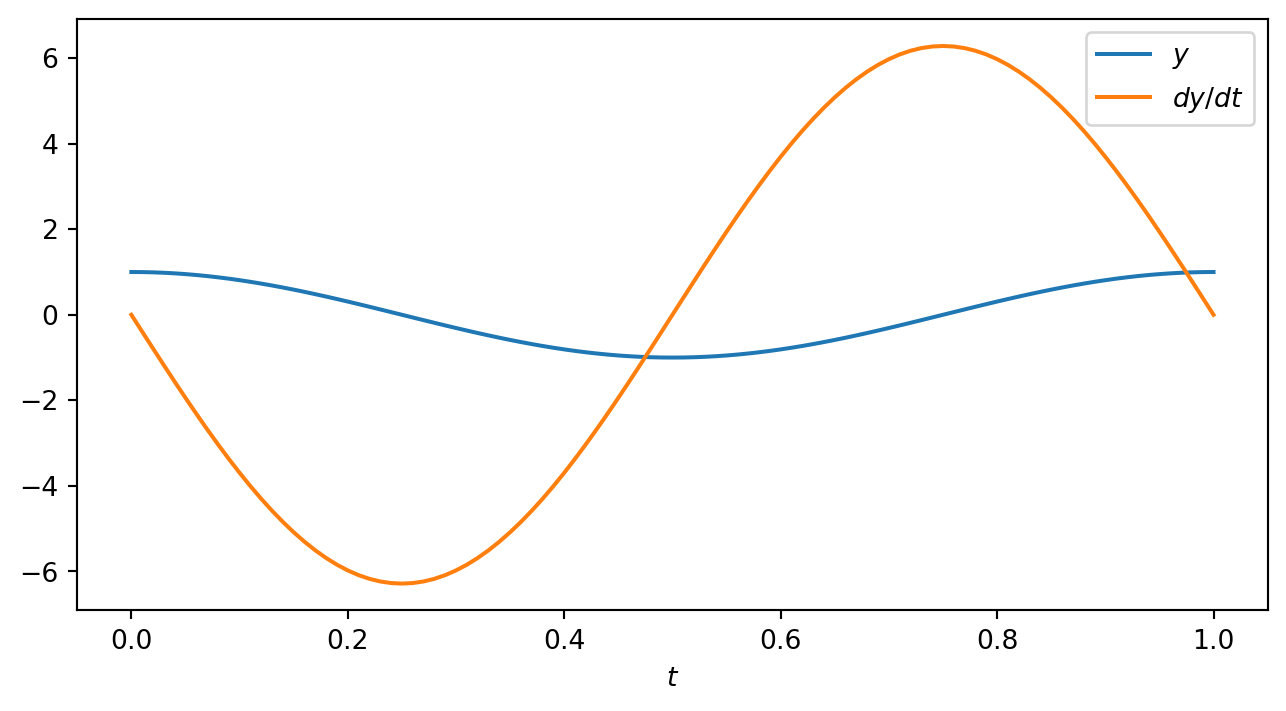
我们可以用四阶R-K方法来对此常微分方程初值问题进行求解(看作两个耦合的一阶方程组)，而Numerov算法的效率更高，因为每一步只需要在格点上计算\(k^2\)和\(S\)，但不能自启动。

Exercise 1 \[ \frac{d^2y}{dx^2} = -4\pi^2y ~~~ y(0) = 1; ~~~ y'(0) = 0; ~~~ y = \cos 2\pi x; \] 用不同的步长 \(h\)，从 \(x = 0\) 积分到 \(x = 1\)，比较Numerov算法与经典四阶R-K算法的效率和精度。

Solution 1. \[ S_i^2 = 4\pi^2;~~~ S_i \equiv 0; ~~~ y_{n+1} = \frac{2(3-5\pi^2h^2)}{(3+\pi^2h^2)}y_n - y_{n-1}; \]

\[ y_0 = y(0) = 1; ~~~ y_1 = ? \]

Taylor expansion to obtain \(y_1\)

Show the code 
var('x h')
var('y', cls = Function)

res = y(h).series(h, 0, 3).removeO().simplify()
Markdown(f'$${latex(res)}$$')

\[\frac{h^{2} \left. \frac{d^{2}}{d \xi^{2}} y{\left(\xi \right)} \right|_{\substack{ \xi=0 }}}{2} + h \left. \frac{d}{d \xi} y{\left(\xi \right)} \right|_{\substack{ \xi=0 }} + y{\left(0 \right)}\]

\[ y_1 \approx y_0 + hy_0 + \frac{h^2}{2}y_0'' = 1 - 2\pi^2h^2 \]

RK: reduce the order:

\[\begin{eqnarray} \left\lbrace \begin{matrix*}[l] \frac{d^2y}{dx^2} = -4\pi^2y \\ y(0) = 1\\ y'(0) = 0 \end{matrix*} \right. \Rightarrow \left\lbrace \begin{matrix*}[l] \frac{dy}{dx} = z \\ \frac{dz}{dx} = -4\pi^2 y \\ y(0) = 1\\ z(0) = 0 \end{matrix*} \right. \end{eqnarray}\]
Show the code 
def ode(x, y):
    res = y.copy()
    res[0] = y[1]
    res[1] = -4*np.pi**2 * y[0]
    return res
  
def rk4(func, x0, y0, h, xp):
    steps = int((xp - x0) / h)
    result = np.zeros((steps + 1, len(y0)))
    xis = np.zeros((steps + 1, 1))
    xi = x0
    yi = y0
    xis[0] = x0
    result[0, :] = yi
    for i in range(steps):
        k1 = func(xi, yi)
        k2 = func(xi + 0.5 * h, yi + 0.5 * h * k1)
        k3 = func(xi + 0.5 * h, yi + 0.5 * h * k2)
        k4 = func(xi + h, yi + h * k3)
        xi = xi + h
        yi = yi + h / 6.0 * (k1 + 2.0 * k2 + 2.0 * k3 + k4)
        xis[i + 1] = xi
        result[i + 1, :] = yi
    return xis, result

h = 0.01
x0 = 0
xp = 1.0

y0 = np.array([1.0, 0.0])

xi, yi = rk4(ode, x0, y0, h, xp)


plt.plot(xi, yi[:, 0], label = r'$y$')
plt.plot(xi, yi[:, 1], label = r'$dy/dt$')
plt.xlabel(r'$t$')
plt.legend()
plt.show()

Show the code 
def numerov(x0, y0, y0p, h, xp):
    steps = int((xp - x0) / h)
    result = np.zeros((steps + 1, 1))
    xis = np.zeros((steps + 1, 1))
    y1 = y0 + h * y0p +  (- 4.0 * np.pi**2.0 * y0) * h**2.0 / 2.0
    result[1] = y1
    result[0] = y0 

    fac = 2.0 * (3.0 - 5.0 * np.pi**2.0 * h**2.0) / (3.0 + np.pi**2.0 * h**2.0)

    xis[0] = x0
    xis[1] = x0 + h
    for i in range(steps - 1):
        j = i + 1
        xis[j + 1] = (j + 1) * h + x0
        result[j + 1] = fac * result[j] - result[j - 1]
    return xis, result

def numerov2(x0, y0, y1, h, xp):
    steps = int((xp - x0) / h)
    result = np.zeros((steps + 1, 1))
    xis = np.zeros((steps + 1, 1))
    result[1] = y1
    result[0] = y0 

    fac = 2.0 * (3.0 - 5.0 * np.pi**2.0 * h**2.0) / (3.0 + np.pi**2.0 * h**2.0)

    xis[0] = x0
    xis[1] = x0 + h
    for i in range(steps - 1):
        j = i + 1
        xis[j + 1] = (j + 1) * h + x0
        result[j + 1] = fac * result[j] - result[j - 1]
    return xis, result

x0 = 0
y0 = 1
y0p = 0
h = 0.01
xp = 1
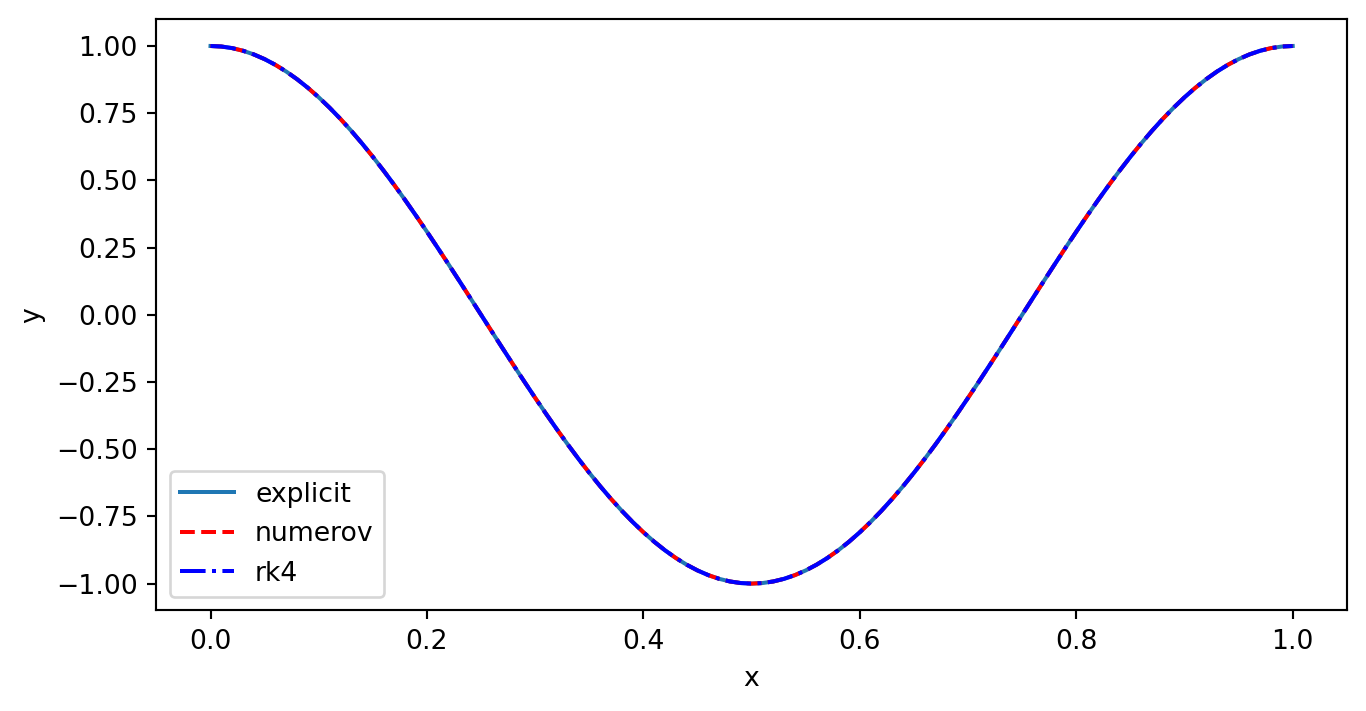
xis, result = numerov(x0, y0, y0p, h, xp)
xis2, result2 = numerov2(x0, y0, yi[1, 0], h, xp)
ex_y = np.cos(2.0 * np.pi * xi[:, 0])

plt.plot(xi, ex_y, label = 'explicit')
plt.plot(xis, result, 'r--', label = 'numerov')
plt.plot(xi, yi[:, 0], 'b-.', label = 'rk4')
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.show()

Show the code 
plt.plot(xi, result[:, 0] - ex_y, label = 'numerov')
plt.plot(xi, result2[:, 0] - ex_y, label = 'numerov2')
plt.plot(xi, yi[:, 0] - ex_y, label = 'rk4')
plt.ylabel('error')
plt.xlabel('x')
plt.legend()
plt.show()

%filename: chapter3_example_0_Numerov.m
%比较Numerov方法与四阶R-K算法
function compare_RK_Numerov
clear all
close all
clc
format long

A=1;
x=0:0.001:A;
y=@(x)cos(2*pi*x); %方程的精确解

h=0.01;
N=fix(A/h); %fix表示取整运算
xx=0:h:N*h;
%-----------四阶R-K算法-------------------
y_rk=zeros(1,N+1);
z_rk=zeros(1,N+1);
tic
f1=@(xx,yy)[yy(2),-4*pi^2*yy(1)]; % 定义 f1，
z0 = [1,0]; 
z1 = myrungekutta(f1, xx, z0);
y_rk = z1(:,1)';   %用四阶RK算法求得的y值
z_rk = z1(:,2)'; 
toc
%------Numerov算法------------
tic
y_n(1)=1;
y_n(2)=y_rk(2);%cos(2*pi*h);%cos(2*pi*h); %y_rk(2);%1-2*pi^2*h^2;%cos(2*pi*h); 
% 1-2*pi^2*h^2 %Numerov算法的精度和启动点的精度有关，
%如采用1-2*pi^2*h^2时精度就和RK算法差不多
for n=2:N
    y_n(n+1)=2*(3-5*pi^2*h^2)/(3+pi^2*h^2)*y_n(n)-y_n(n-1);
end
toc

a=0.9;
n=round(a/h);
fprintf('y(a)的精确值为：%f\n',y(a));
fprintf('四阶R-K法求得的值为：%f\n',y_rk(n+1));
fprintf('四阶R-K法的误差为：%f\n',y(a)-y_rk(n+1));
fprintf('Numerov法求得的值为：%f\n',y_n(n+1))
fprintf('Numerov法的误差为：%f\n',y(a)-y_n(n+1));

figure;plot(x,y(x),'b',xx,y_rk,'r',xx,y_n,'k')%精确解,RK算法,Numerov算法
legend('精确解','RK','Numerov')
figure;plot(xx,y_rk-y(xx),'r',xx,y_n-y(xx),'b') %RK算法与Numerov算法误差比较图
legend('RK','Numerov')
title('RK算法与Numerov算法误差比较图')

function z = myrungekutta(f, xx, z)
n = length(xx);
h = xx(2)-xx(1);
for i = 1:n-1
    k1 = f(xx(i), z(i,:));
    k2=f(xx(i)+0.5*h, z(i,:) + h*k1/2);
    k3=f(xx(i)+0.5*h, z(i,:) + h*k2/2);
    k4=f(xx(i)+h, z(i,:) + h*k3);
    z(i+1,:)=z(i,:) + (k1 + 2*k2 + 2*k3 + k4)*h/6;
end
Note

Numerov算法只针对特定二阶常微分方程，使用上有局限性。

3 边值问题的数值求解

本节介绍求解两点边值问题 \[ \begin{eqnarray} \left\lbrace \begin{matrix*}[l] y'' = f(x, y, y') \\ y(a) = \alpha, y(b) = \beta, \end{matrix*} \right. \end{eqnarray} \tag{1}\] 的数值解法。

当 \(f\) 关于 \(y\) 和 \(y'\) 是线性时，式(Equation 1)为线性两点边值问题 \[ \begin{eqnarray} \left\lbrace \begin{matrix*}[l] y'' + p(x)y' + q(x)y = f(x) \\ y(a) = \alpha, y(b) = \beta, \end{matrix*} \right. \end{eqnarray} \tag{2}\]

3.1 迭加法

对于线性边值问题(Equation 2)，一个简单又实用的方法是用解析的思想，将它转化为两个初值问题：

\[ \left\lbrace \begin{matrix*}[l] y'' + p(x)y' + q(x)y = f(x), \\ y(a) = \alpha, y(b) = \beta, \end{matrix*} \right. ~~ \longrightarrow ~~ \begin{matrix*}[l] \left\lbrace \begin{matrix*}[l] y_1'' + p(x)y_1' + q(x)y_1 = f(x), \\ y_1(a) = \alpha, y_1'(a) = 0, \end{matrix*} \right.\\ \left\lbrace \begin{matrix*}[l] y_2'' + p(x)y_2' + q(x)y_2 = 0, \\ y_2(a) = 0, y'_2(a) = 1, \end{matrix*} \right. \end{matrix*} \] 求得这两个初值问题的解 \(y_1(x)\) 和 \(y_2(x)\) , 若 \(y_2(b)\neq 0\)，容易验证

\[ y(x) = y_1(x) + \frac{\beta - y_1(b)}{y_2(b)}y_2(x) \tag{3}\] 为线性两点边值问题(Equation 2)的解，此种方法称为迭加法。

3.2 打靶法

对于非线性边值问题，迭加法无能为力。打靶法的基本原理是将两点边值问题（1）转化为下列形式的初值问题

\[ \left\lbrace \begin{matrix*}[l] y'' = f(x, y, y'), \\ y(a) = \alpha, ~~ y'(a) = s_k \end{matrix*} \right. \tag{4}\]

这里的 \(s_k\) 为 \(y\) 在 \(a\) 处的斜率。令 \(z = y'\) ，上述二阶方程可降为一阶方程组 \[ \left\lbrace \begin{matrix*}[l] y' = z, \\ z' = f(x, y, z), \\ y(a) = \alpha, ~~ z(a) = s_k \end{matrix*} \right. \tag{5}\] 因此，边值问题变成求合适的 \(s_k\)，使上述方程组初值问题的解满足原边值问题的右端边界条件\(y(b) = \beta\)，从而得到边值问题的解。这样，把一个两点边值问题的数值解问题转化为一阶方程组初值问题的数值解问题。方程组初值问题的所有数值方法在这里都可以使用。

❓ 问题的关键是如何去找合适的初始斜率的试探值？

对给定的 \(s_k\) ，设初值问题(Equation 4)的解为\(y(x,s_k)\)，它是\(s_k\)的隐函数。假设\(y(x, s_k)\)随\(s_k\)是连续变化的，记为\(y(x, s)\)，于是我们要找的\(s_k\)就是方程 \[ \underbrace{y(b, s) - \beta}_\text{roots function} = 0 \] 的根。可以用第2章的弦割法求上述方程的根。 \[ x_k = x_{k-1} - \frac{F(x_{k-1})(x_{k-1} - x_{k-2})}{F(x_{k-1}) - F(x_{k - 2})} \]

\[ s_k = s_{k-1} - \frac{s_{k - 1} - s_{k - 2}}{y(b, s_{k - 1}) - y(b, s_{k - 2})}[y(b, s_{k - 1}) - \beta], ~~ k = 2, 3, ... \tag{6}\]

这样，可以按下面简单的计算过程进行求解：

  1. 先给定两个初始斜率\(s_0\), \(s_1\)（弦割法的两个启动点），分别作为初值问题(Equation 5)的初始条件。
  2. 用一阶方程组的数值方法求解它们，分别得到区间右端点的函数的计算值 \(y(b,s_0)\) 和\(y(b, s_1)\)。如果\(|y(b, s_0) - \beta| < \varepsilon\)或\(|y(b, s_1) - \beta| < \varepsilon\)，则以\(y(b,s_0)\)或\(y(b,s_1)\)作为两点边值问题的解。否则用割线法(Equation 6)求\(s_2\)，同理得到\(y(b,s_2)\)，再判断它是否满足精度要求\(|y(b, s_2) - \beta| < \varepsilon\)。

如此重复，直到某个\(s_k\)满足\(|y(b, s_k) - \beta| < \varepsilon\)，此时得到的\(y(x_i)\)和\(y_i' = z(x_i)\)就是边值问题的解函数值和它的一阶导数值。上述方程好比打靶，\(s_k\)作为斜率为子弹的发射，\(y(b)\)为靶心，故称为打靶法。

打靶法的算法实现
  1. 给定初始点的斜率猜测值S1；
  2. 用常微分方程的初值问题解法（如RK算法）求解y(b,S1);
  3. 给出另一个斜率猜测值S2作为弦割法的第二个启动点;
  4. 用常微分方程的初值问题解法（如RK算法）求解y(b,S2);
  5. IF (abs(y(b,S1)-y(b))<精度 \(\varepsilon\) ), y(x)=y(x,S1);
  6. IF (abs(y(b,S2)-y(b))<精度 \(\varepsilon\) ), y(x)=y(x,S2); else
  7. 利用弦割法迭代公式求出下一个斜率S3；
  8. 用常微分方程的初值问题解法（如RK算法）求解y(b,S3);
  9. IF (abs(y(b,S3)-y(b))<精度 \(\varepsilon\) ), y(x)=y(x,S3); else S1=S2; S2=S3；回到第7步
  10. 得到边值问题的解y(x)=y(x,S3);

%%{ init : { "theme" : "neutral", "flowchart" : { "curve" : "linear" }}}%%
flowchart TD
A("guess S1, S2")
B("solve y(b, S1), y(b, S2)")
C{"IF (abs(y(b,S1)-y(b)) < eps"}
D{"IF (abs(y(b,S2)-y(b)) < eps"}
E("calculate S3")
F("solve y(b, S3)")
G{"IF (abs(y(b,S3)-y(b)) < eps"}
H("y(x) = y(x, S3)")
I("S1 = S2; S2 = S3")
C1("y(x) = y(x, S1)")
D1("y(x) = y(x, S2")

A --> B --> C -->|true| C1
C-->|false|D -->|true|D1
D-->|false|E --> F --> G -->|true|H
G-->|false|I --> F

Example 1

Example 1 用迭加法和打靶法求解下述线性边值问题

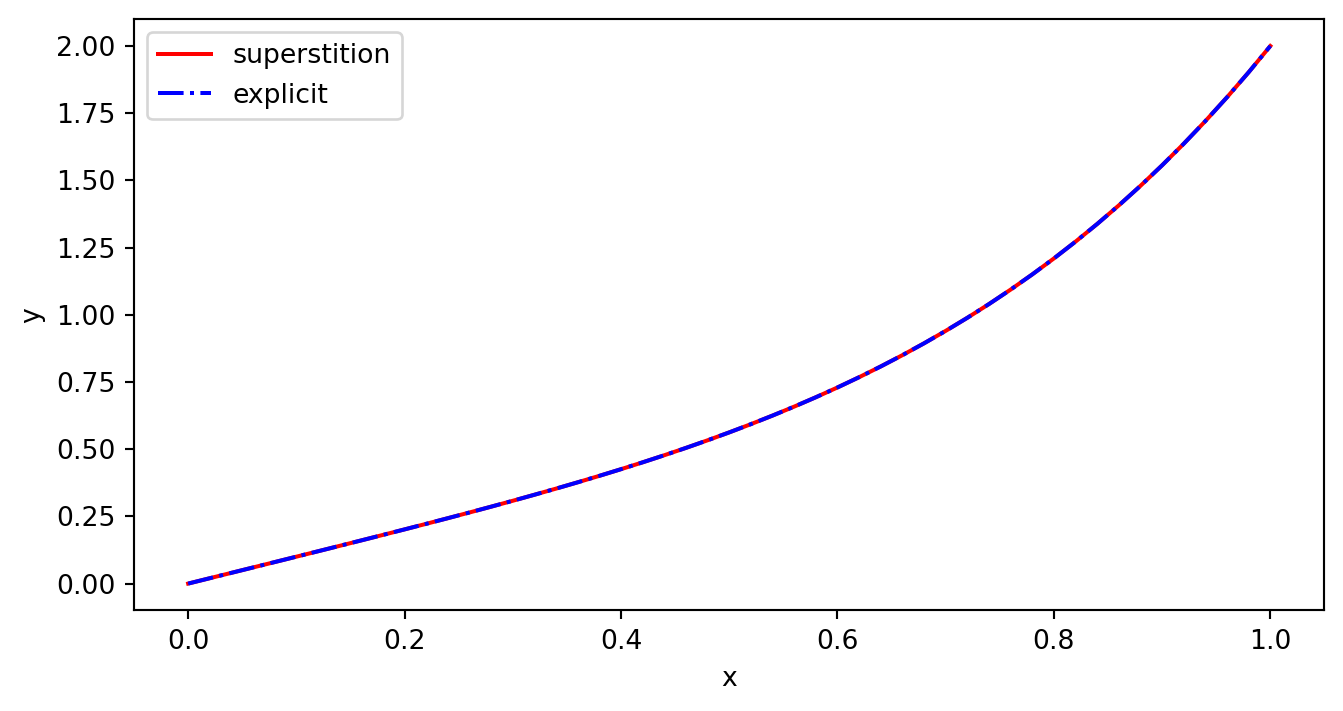
\[ \left\lbrace \begin{matrix*}[l] y'' + xy' - 4y = 12x^2 - 3x, ~~ 0<x<1, \\ y(0) = 0, ~~ y(1) = 2 \end{matrix*} \right. \] 其解的解析表达式为\(y(x) = x^4 + x\)。

solution:

  1. （迭加法）先将该线性边值问题转化为两个初值问题

\[ \begin{matrix*}[l] \left\lbrace \begin{matrix*}[l] y_1'' + xy_1' -4 y_1 = 12x^2 - 3x, \\ y_1(0) = 0, ~~ y_1'(0) = 0, \end{matrix*} \right.\\ \left\lbrace \begin{matrix*}[l] y_2'' + xy_2' -4y_2 = 0, \\ y_2(0) = 0, ~~ y_2'(0) = 1 \end{matrix*} \right. \end{matrix*} \]

let \(z_1 = y_1', z_2 = y_2'\), 将上述两个边值问题分别降为一阶方程组初值问题

\[ \begin{matrix*}[l] \left\lbrace \begin{matrix*}[l] y_1' = z_1, \\ z_1' = -xz_1 + 4y_1 + 12x^2 - 3x, \\ y_1(0) = 0, ~~ z_1(0) = 0 \end{matrix*} \right. \\ \left\lbrace \begin{matrix*}[l] y_2' = z_2, \\ z_2' = -xz_2 + 4y_2, \\ y_2(0) = 0, ~~ z_2(0) = 1 \end{matrix*} \right. \end{matrix*} \] Refer (Equation 3) with \(b = 1, ~~\beta = 2\)

取 \(h = 0.02\)，用经典R-K法分别求这两个方程组解\(y_1(x)\)和\(y_2(x)\)的计算值\(y_{1i}\)和\(y_{2i}\)，然后按(Equation 3)得精确解 \[ y(x) = y_1(x) + \frac{2 - y_1(1)}{y_2(1)}y_2(x) \] Code:

%filename: chapter3_example_1_superposition_method.m
%用迭加法求解线性常微分方程的边值问题，其中用到了四阶R-K算法
function superposition_method
clear
clc,close all
format long

A=1;
x=0:0.001:A;
y=@(x)(x.^4+x); %方程的精确解

XL=0.0;       %左边界点
XU=1.0;       %右边界点
h=0.02;           
N=(XU-XL)/h;
xx=0:h:N*h;

YL= 0.0;              %边界点函数值

% y_rk1=zeros(1,N+1);
% z_rk1=zeros(1,N+1);
% 
% y_rk2=zeros(1,N+1);
% z_rk2=zeros(1,N+1);
% 
% yy_rk=zeros(1,N+1);

%-----------四阶R-K算法-------------------
f1=@(xx,yy)[yy(2),-xx*yy(2)+4*yy(1)+12*xx^2-3*xx]; % 定义 f1，
z1 = [0,0];        %第一个常微分方程组的初值
z1 = myrungekutta(f1, xx, z1);
y_rk1 = z1(:,1);   %用四阶RK算法求得的y值
z_rk1 = z1(:,2); 

%----------第二个方程组的解，求右边界的函数值及误差函数--------------------
f2=@(xx,yy)[yy(2),-xx*yy(2)+4*yy(1)]; % 定义 f1，
z2 = [0,1];        %第二个常微分方程组的初值
z2 = myrungekutta(f2, xx, z2);
y_rk2 = z2(:,1);   %用四阶RK算法求得的y值
z_rk2 = z2(:,2); 

yy_rk=y_rk1+y_rk2*(2-y_rk1(end))/y_rk2(length(xx));

for a=0:0.2:1.0;
n=round(a/h);
error1(n+1)=y(a)-yy_rk(n+1);
fprintf('%11.10f\t',a,y_rk1(n+1),y_rk2(n+1),yy_rk(n+1),y(a),abs(error1(n+1)));
fprintf('\n');
end


for a=0:h:N*h;
n=round(a/h);
error(n+1)=y(a)-yy_rk(n+1);
end
fprintf('迭加法求得y(1)的值为：%f\n',yy_rk(N+1));
fprintf('迭加法求得y(1)值的误差为：%f\n',y(1)-yy_rk(N+1));

subplot(2,1,1),plot(x,y(x),'b',xx,yy_rk,'r')%精确解
title('迭加法结果与精确解比较')
legend('精确解','迭加法','Location','best')
subplot(2,1,2),plot(xx,error,'r')  %打靶法误差曲线
title('迭加法误差曲线')
hold off


function z = myrungekutta(f, xx, z)
n = length(xx);
h = xx(2)-xx(1);
for i = 1:n-1
    k1 = f(xx(i), z(i,:));
    k2=f(xx(i)+0.5*h, z(i,:) + h*k1/2);
    k3=f(xx(i)+0.5*h, z(i,:) + h*k2/2);
    k4=f(xx(i)+h, z(i,:) + h*k3);
    z(i+1,:)=z(i,:) + (k1 + 2*k2 + 2*k3 + k4)*h/6;
end
Show the code 
def ode1(x, y):
    res = y.copy()
    res[0] = y[1]
    res[1] = -x * y[1] + 4 * y[0] + 12 * x**2 - 3 * x
    return res

def ode2(x, y):
    res = y.copy()
    res[0] = y[1]
    res[1] = - x * y[1] + 4 * y[0]
    return res
  
y00 = np.array([0, 0])
y01 = np.array([0, 1])

h = 0.02
x0 = 0
xp = 1
xi1, yi1 = rk4(ode1, x0, y00, h, xp)
xi2, yi2 = rk4(ode2, x0, y01, h, xp)

y1 = yi1[:, 0]
y2 = yi2[:, 0]

yfin = y1 + (2.0 - y1[-1]) / y2[-1] * y2

y_ex = xi1**4.0 + xi1

plt.plot(xi1, yfin, 'r-', label = 'superstition')
plt.plot(xi1, y_ex, 'b-.', label = 'explicit')
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.show()

Show the code 
plt.plot(xi1[:, 0], y_ex[:, 0] - yfin)
plt.xlabel('x')
plt.ylabel('err')
plt.show()

shooting method

\[ \left\lbrace \begin{matrix*}[l] y' = z; \\ z' = -xz + 4y + 12x^2 - 3x; \\ y(0) = 0, ~~ z_1(0) = S, \end{matrix*} \right. \]

Code:

%filename: chapter3_example_1_shooting_method.m
%用打靶法求解常微分方程的边值问题，其中用到了弦割法和四阶R-K算法;
function shooting_method_RK_secant
clear
clc
close all
format long

A=1;
x=0:0.001:A;
y=@(x)(x.^4+x); %方程的精确解

DL=5*10^-27;  %误差判断标准，用于弦割法
XL=0.0;       %左边界点
XU=1.0;       %右边界点
h=0.02;           
N=(XU-XL)/h;
xx=XL:h:XL+N*h;
%D = 1;               %初始化误差
YL= 0.0;              %左边界点函数值
YU= 2.0;              %右边界点函数值
S0= 1000;              %XL处斜率的猜测值，弦割法第一个启动点
S1= 4;              %第二个斜率猜测值，作为弦割法的第二个启动点

%-----------四阶R-K算法,将求解放在循环外部-------------------
%---------第一个试探解，求右边界的函数值及误差函数-------------------
f=@(xx,yy)[yy(2);-xx*yy(2)+4*yy(1)+12*xx^2-3*xx]; % 定义 f1，
z1 = [YL;S0]; 
z1 = myrungekutta(f, xx, z1);
y_rk1 = z1(1,:)';   %用四阶RK算法求得的y值
z_rk1 = z1(2,:)'; 
F0=y_rk1(end)-YU; %用四阶RK算法得到的XU点的函数值与边界条件的差值
%----------第二个试探解，求右边界的函数值及误差函数--------------------
z2 = [YL;S1]; 
z2 = myrungekutta(f, xx, z2);
y_rk2 = z2(1,:)';   %用四阶RK算法求得的y值
z_rk2 = z2(2,:)'; 
F1=y_rk2(end)-YU; %用四阶RK算法得到的XU点的函数值与边界条件的差值
if (abs(F1)>abs(F0))
    y_rk=y_rk1;
else
    y_rk=y_rk2;
end
nn=0; %迭代次数
%abs(y_rk(end)-YU)
while(abs(y_rk(end)-YU)>DL)
    nn=nn+1
    S2=S1-F1*(S1-S0)/(F1-F0); %弦割法求根
    S0=S1;
    S1=S2;
    F0=F1;
    y_rk1=y_rk;
%----------第三或更高次的试探解，求右边界的函数值及误差函数--------------------
    z2 = [YL;S1]; 
    z2 = myrungekutta(f, xx, z2);
    y_rk2 = z2(1,:)';   %用四阶RK算法求得的y值
    z_rk2 = z2(2,:)'; 
    F1=y_rk2(end)-YU %用四阶RK算法得到的XU点的函数值与边界条件的差值
    if (abs(F1)>abs(F0))
        y_rk=y_rk1;
    else
        y_rk=y_rk2;
    end
    %abs(y_rk(end)-YU)
end

for a=XL:h:XL+N*h;
n=round((a-XL)/h);
error(n+1)=y(a)-y_rk(n+1);
end
fprintf('打靶法求得y(1)的值为：%f\n',y_rk(N+1));
fprintf('打靶法求得y(1)值的误差为：%f\n',y(1)-y_rk(N+1));
fprintf('打靶法的迭代次数为：%f\n',nn);

subplot(2,1,1),plot(x,y(x),'b',xx,y_rk,'r')%精确解与数值解
title('打靶法结果与精确解比较')
legend('精确解','打靶法','Location','best')
subplot(2,1,2),plot(xx,error,'r')  %打靶法误差曲线
title('打靶法误差曲线')
hold off
%vpa(error(end),28)

function z = myrungekutta(f, xx, z)
n = length(xx);
h = xx(2)-xx(1);
for i = 1:n-1
    k1 = f(xx(i), z(:,i));
    k2=f(xx(i)+0.5*h, z(:,i) + h*k1/2);
    k3=f(xx(i)+0.5*h, z(:,i) + h*k2/2);
    k4=f(xx(i)+h, z(:,i) + h*k3);
    z(:,i+1)=z(:,i) + (k1 + 2*k2 + 2*k3 + k4)*h/6;
end
Show the code 
def shooting(ode, x0, y0, h, xp, yp, eps):
    s1 = 0.1
    s2 = 0.2
    y00 = np.array([y0, 0.0])
    while true:
        y00[1] = s1
        x1, y1 = rk4(ode, x0, y00, h, xp)
        y00[1] = s2
        x2, y2 = rk4(ode, x0, y00, h, xp)
        y11 = y1[:, 0]
        y22 = y2[:, 0]
        if (np.abs(y11[-1] - yp) < eps):
            return x1, y11
        if (np.abs(y22[-1] - yp) < eps):
            return x2, y22
        s3 = s2 - (s2 - s1) / (y22[-1] - y11[-1]) * (y22[-1] - yp)
        print(s3)
        y00[1] = s3
        x3, y3 = rk4(ode, x0, y00, h, xp)
        y33 = y3[:, 0]
        if (np.abs(y33[-1] - yp) < eps):
            return x3, y33
        s1 = s2
        s2 = s3

def ode(x, y):
    res = y.copy()
    res[0] = y[1]
    res[1] = -x * y[1] + 4 * y[0] + 12 * x**2 - 3 * x
    return res

x0 = 0
xp = 1

y0 = 0
yp = 2

h = 0.02
eps = 1e-6

xx, yy = shooting(ode, x0, y0, h, xp, yp, eps)

plt.plot(xx, yy)
plt.xlabel('x')
plt.ylabel('y')
plt.show()
1.0000000334999262

Show the code 
plt.plot(xx, y_ex[:, 0] - yy)
plt.xlabel('x')
plt.ylabel('err')
plt.show()

Example 2:

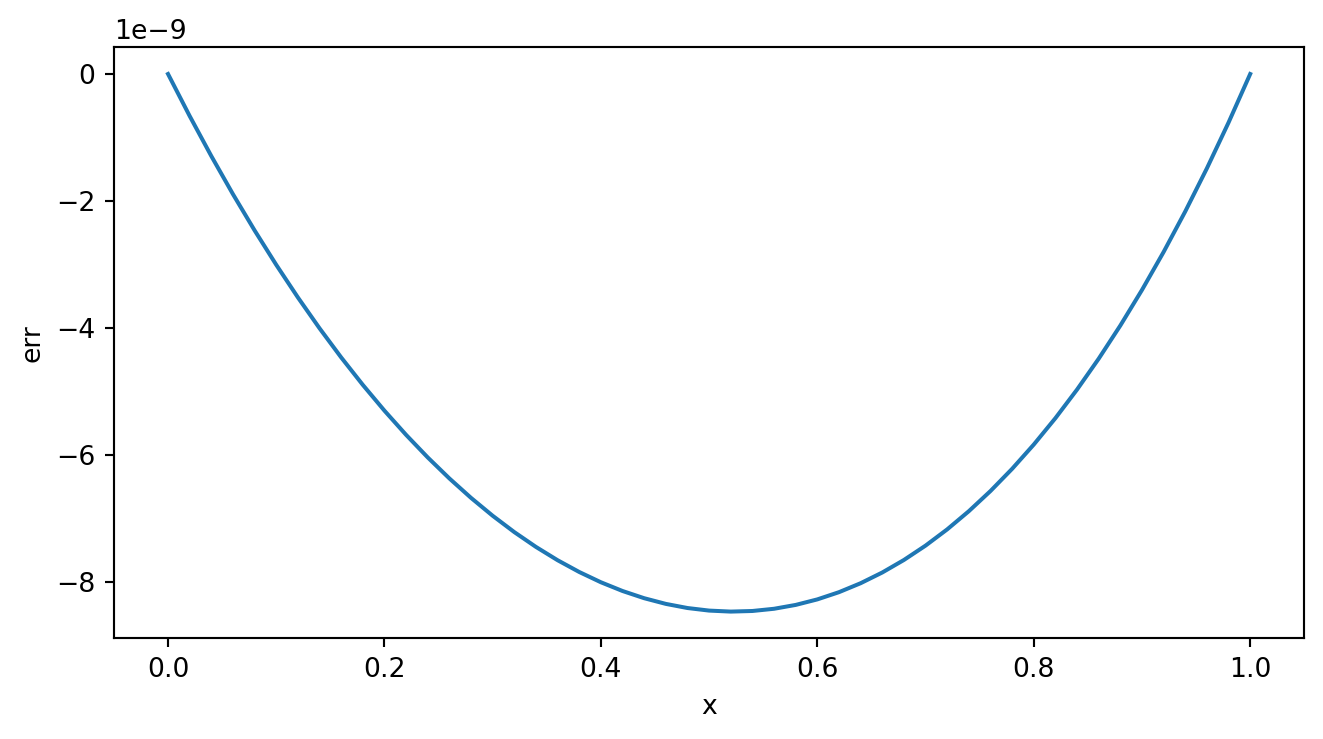
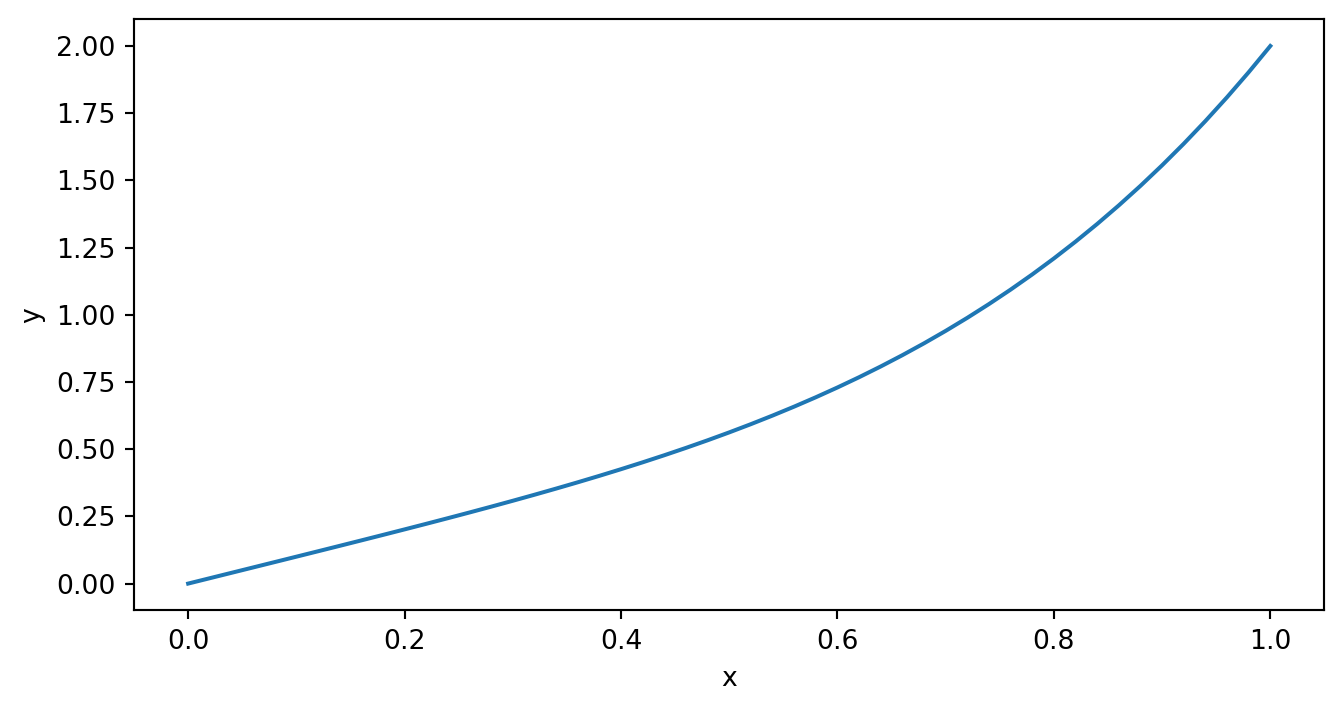
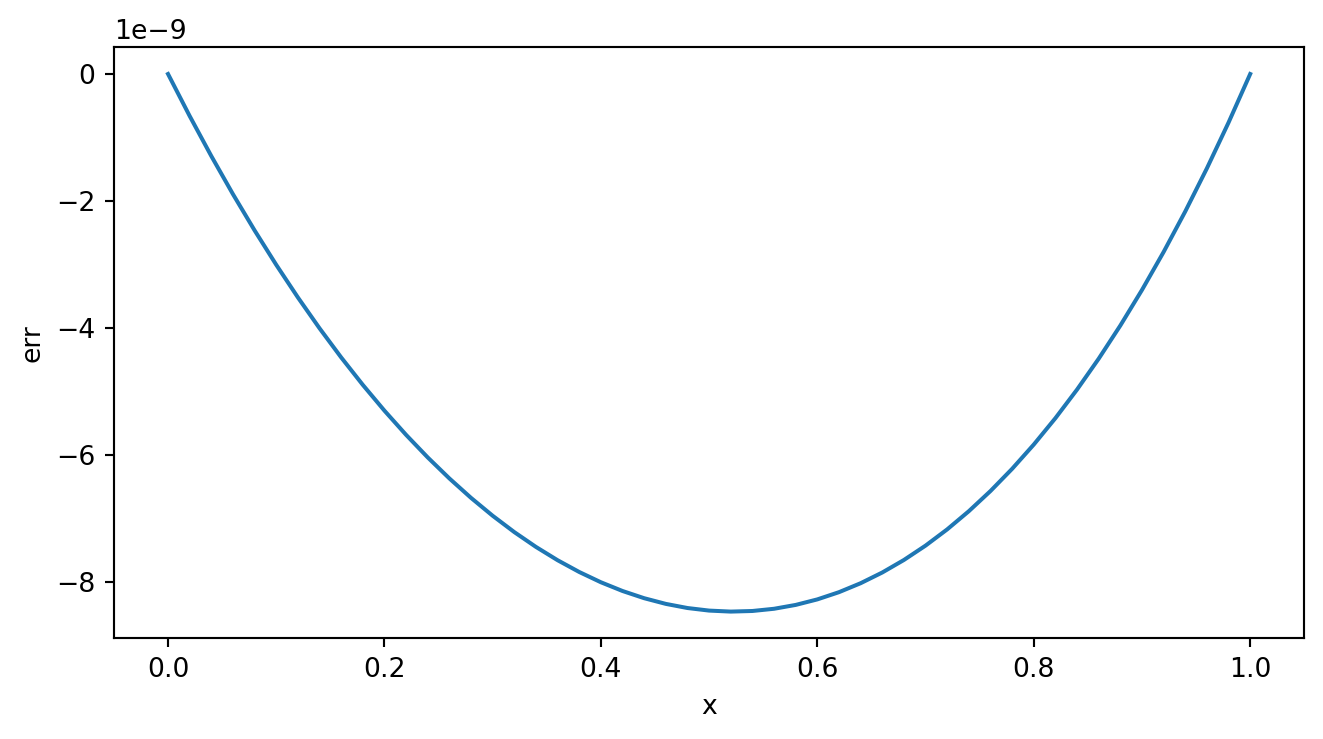
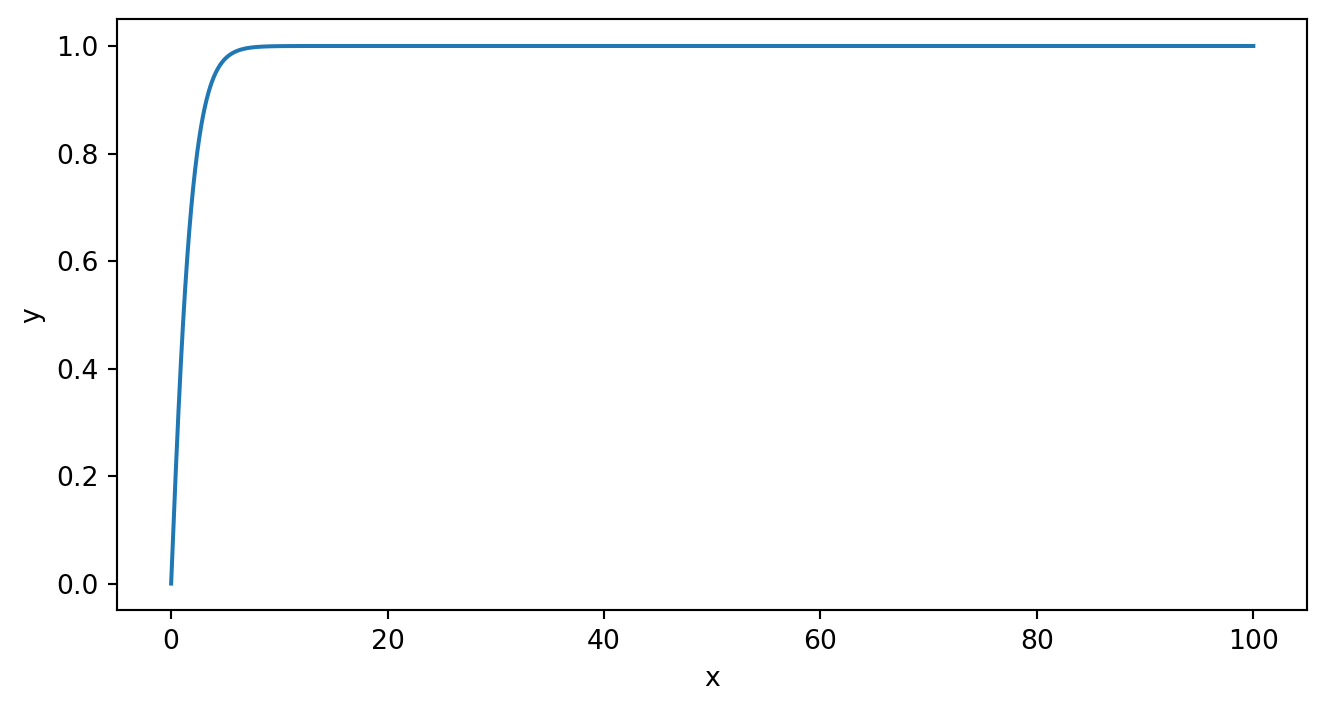
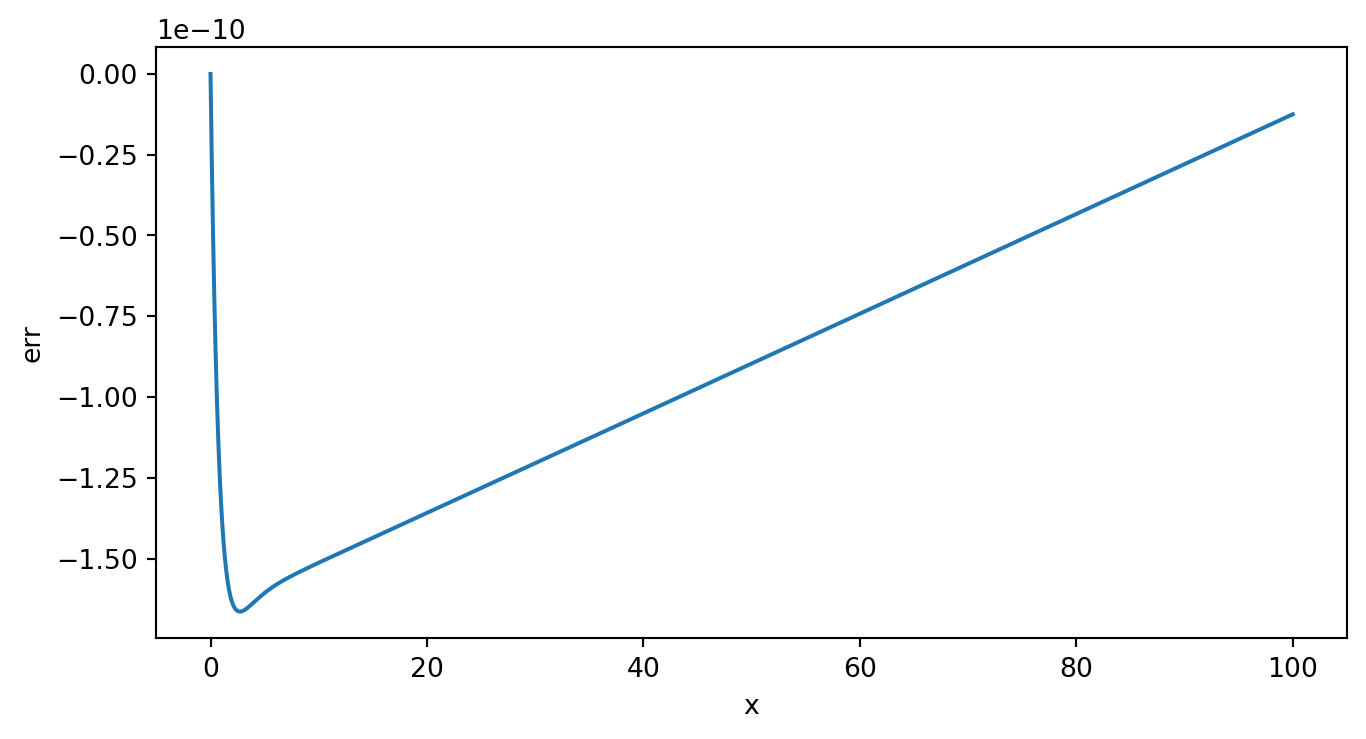
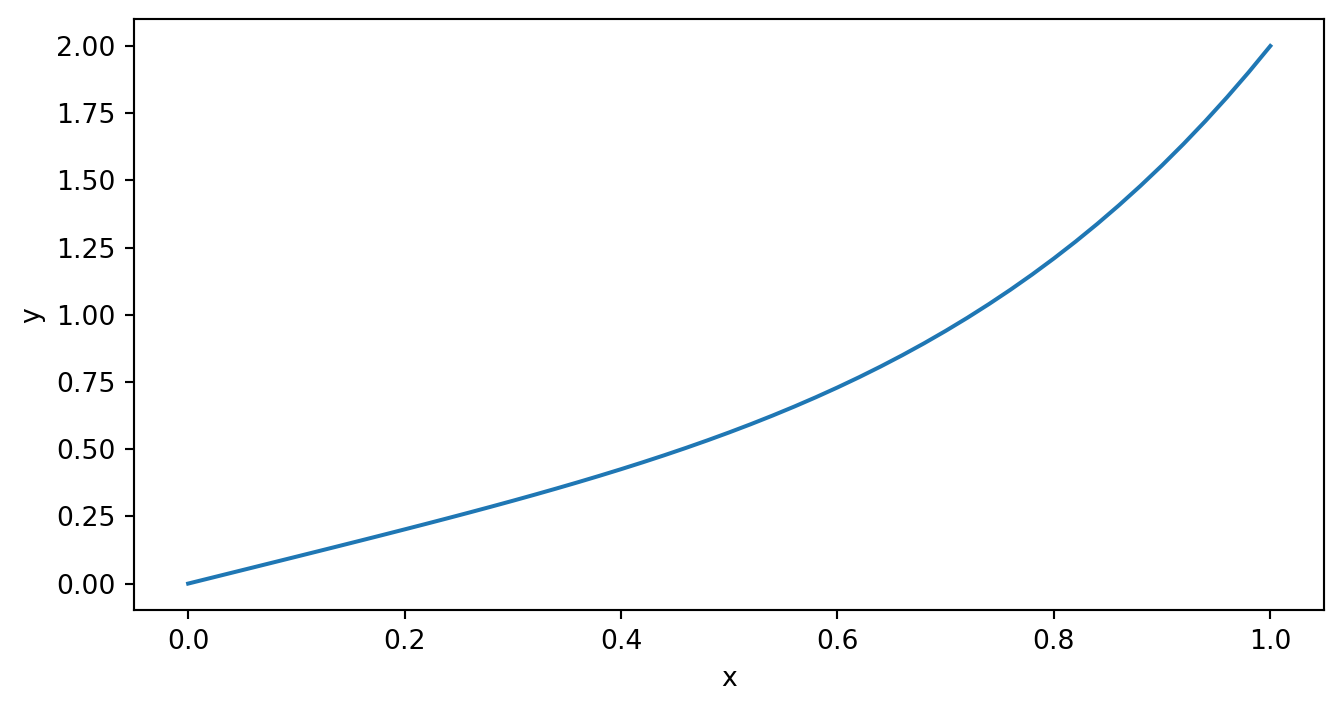
例2. 我们考虑电荷分布为 \(\rho(r) = \frac{1}{8\pi}e^{-r}\) 的电势分布 \[ Q = \int \rho(r)dr^3 = \int_0^\infty p(r)4\pi r^2dr = 1\] 此问题的精确解为 \[\phi(r) = 1-\frac{1}{2}(r+2)e^{-r}\]

\[ \frac{d^2\phi}{dr^2} = -4\pi r \rho = -\frac{1}{2}re^{-r} \] 利用打靶法求解 \[ \left\lbrace \begin{matrix*}[l] \frac{d^2\phi}{dr^2} = -\frac{1}{2}re^{-r} \\ \phi(0) = 0, ~~ \phi(\infty) = 1 \end{matrix*} \right. \longrightarrow \left\lbrace \begin{matrix*}[l] \phi' = z \\ z' = -\frac{1}{2}re^{-r} \phi(0) = 0, ~~ z(0) = S \end{matrix*} \right. \]

%filename: chapter3_example_2_shooting_method_poission.m
%用打靶法求解Poisson方程的边值问题，其中用到了弦割法和四阶R-K算法;
function shooting_method_RK_secant
clear
clc,close all
format long

A=20;
x=0:0.001:A;
y=@(x)(1-0.5*(x+2).*exp(-x)); %方程的精确解

DL=0.5*10^-10;  %误差判断标准，用于弦割法
XL=0.0;        %左边界点
XU=A;          %右边界点
h=0.02;           
N=(XU-XL)/h;
xx=XL:h:XL+N*h;
YL= 0.0;              %左边界点函数值
YU= 1.0;              %右边界点函数值
S0= 350;              %XL处斜率的猜测值，弦割法第一个启动点
S1= -4500;              %第二个斜率猜测值，作为弦割法的第二个启动点

% y_rk1=zeros(1,N+1);
% z_rk1=zeros(1,N+1);
% y_rk2=zeros(1,N+1);
% z_rk2=zeros(1,N+1);
% y_rk=zeros(1,N+1);
% z_rk=zeros(1,N+1);

%-----------四阶R-K算法,将求解放在循环外部-------------------
%---------第一个试探解，求右边界的函数值及误差函数-------------------
f=@(xx,yy)[yy(2),-0.5*xx*exp(-xx)]; % 定义 f1， % 定义 f1，
z1 = [YL,S0]; 
z1 = myrungekutta(f, xx, z1);
y_rk1 = z1(:,1);   %用四阶RK算法求得的y值
% z_rk1 = z1(:,2); 
F0=y_rk1(end)-YU; %用四阶RK算法得到的XU点的函数值与边界条件的差值
%----------第二个试探解，求右边界的函数值及误差函数--------------------
z2 = [YL,S1]; 
z2 = myrungekutta(f, xx, z2);
y_rk2 = z2(:,1);   %用四阶RK算法求得的y值
% z_rk2 = z2(:,2); 
F1=y_rk2(end)-YU; %用四阶RK算法得到的XU点的函数值与边界条件的差值
if (abs(F1)>abs(F0))
    y_rk=y_rk1;
else
    y_rk=y_rk2;
end
nn=0;
while(abs(y_rk(end)-YU)>DL)
    nn=nn+1;
    S2=S1-F1*(S1-S0)/(F1-F0); %弦割法求根
    S0=S1;
    S1=S2;
    F0=F1;
    y_rk1=y_rk;
%----------第三或更高次的试探解，求右边界的函数值及误差函数--------------------
    z2 = [YL,S1]; 
    z2 = myrungekutta(f, xx, z2);
    y_rk2 = z2(:,1);   %用四阶RK算法求得的y值
%     z_rk2 = z2(:,2); 
    F1=y_rk2(end)-YU; %用四阶RK算法得到的XU点的函数值与边界条件的差值
    if (abs(F1)>abs(F0))
        y_rk=y_rk1;
    else
        y_rk=y_rk2;
    end
    %abs(y_rk(end)-YU)
end

for a=XL:h:XL+N*h;
n=round((a-XL)/h);
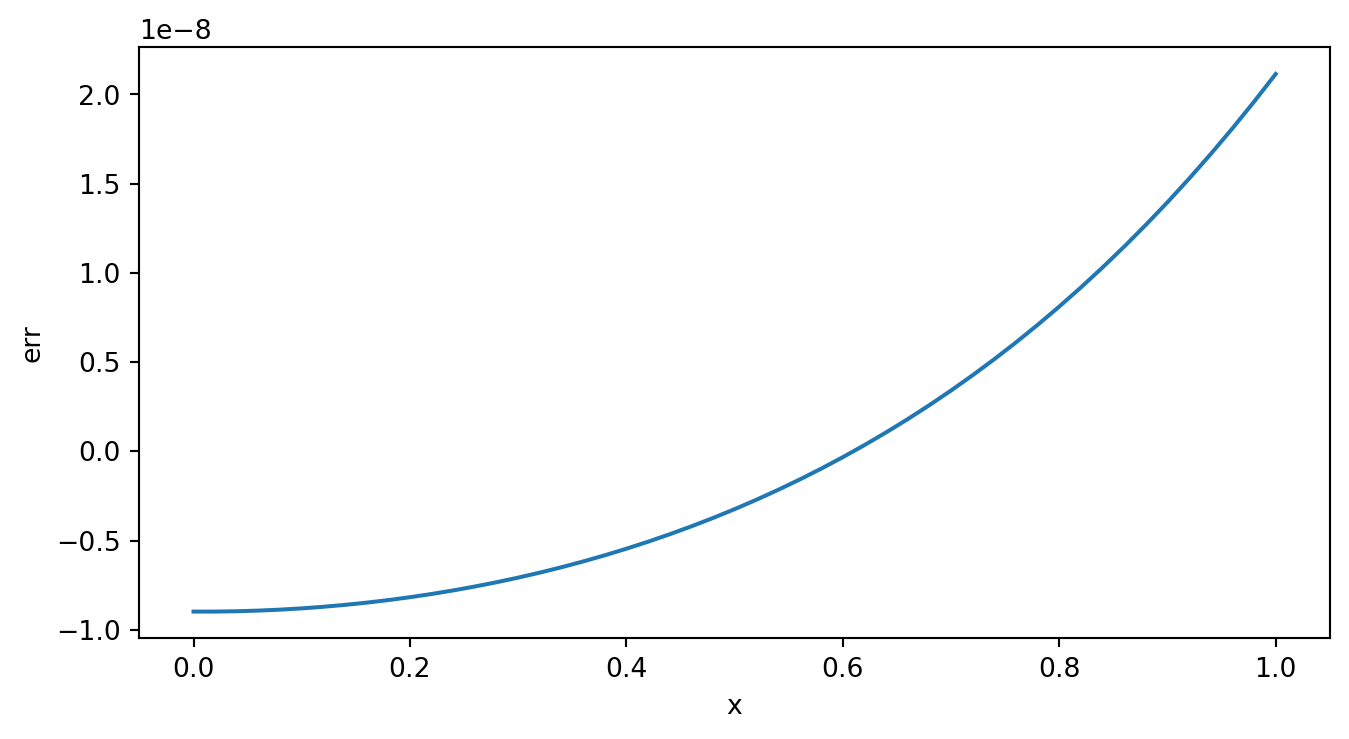
error(n+1)=y(a)-y_rk(n+1);
end
fprintf('打靶法求得y(100)的值为：%f\n',y_rk(N+1));
fprintf('打靶法求得y(100)值的误差为：%f\n',y(A)-y_rk(N+1));
fprintf('打靶法的迭代次数为：%f\n',nn);

subplot(2,1,1),plot(x,y(x),'b',xx,y_rk,'r')%精确解
title('打靶法结果与精确解比较')
legend('精确解','打靶法','Location','best')
subplot(2,1,2),plot(xx,error,'r')  %打靶法误差曲线
title('打靶法误差曲线')
hold off


function z = myrungekutta(f, xx, z)
n = length(xx);
h = xx(2)-xx(1);
for i = 1:n-1
    k1 = f(xx(i), z(i,:));
    k2=f(xx(i)+0.5*h, z(i,:) + h*k1/2);
    k3=f(xx(i)+0.5*h, z(i,:) + h*k2/2);
    k4=f(xx(i)+h, z(i,:) + h*k3);
    z(i+1,:)=z(i,:) + (k1 + 2*k2 + 2*k3 + k4)*h/6;
end
Show the code 
def ode(x, y):
    res = y.copy()
    res[0] = y[1]
    res[1] = -0.5 * x * np.exp(-x)
    return res
  
x0 = 0
xp = 100

y0 = 0
yp = 1

h = 0.02
eps = 1e-6

xx, yy = shooting(ode, x0, y0, h, xp, yp, eps)

plt.plot(xx, yy)
plt.xlabel('x')
plt.ylabel('y')
plt.show()
0.49999999991512944

Show the code 
y_ex = 1.0 - 0.5 * (xx + 2.0) * np.exp(-xx)
plt.plot(xx, y_ex[:, 0] - yy)
plt.xlabel('x')
plt.ylabel('err')
plt.show()

4 不同边界条件下的边值问题求解

常微分方程具有如下常见的三种边界条件：

  1. \(y(a) = \alpha,~~ y(b) = \beta\) — 第一类
  2. \(y'(a) = \alpha,~~ y'(b) = \beta\) — 第二类
  3. \(y'(a) - \alpha_0y(a) = \beta_0, ~~ y'(b) - \alpha_1 y(b) = \beta_1\) — 第三类
第一类

\[ \left\lbrace \begin{matrix*}[l] y'' = f(x, y, y') \\ y(a) = \alpha, ~~ y'(a) = s_k \end{matrix*} \right. \]

第二类

\[ \left\lbrace \begin{matrix*}[l] y'' = f(x, y, y') \\ y(a) = s_k, ~~ y'(a) = \alpha \end{matrix*} \right. \]

第三类

仍可转化为考虑初值问题，取\(y'_0 = \beta_0 + \alpha_0 y_0\)，以 \(y_0\)为待定参数。打靶法如下： \[ \left\lbrace \begin{matrix*}[l] y'' = f(x, y, y') \\ y(a) = y_0, ~~ y'_0 = \beta_0 + \alpha_0 y_0, \\ y'(b) = \frac{y(b) - y(b - h)}{h} = \alpha_1 y(b) + \beta_1 \end{matrix*} \right. \]

Example 3

\[ \left\lbrace \begin{matrix*}[l] y'' + xy' -4y = 12x^2 - 3x, ~~ 0<x<1, \\ y'(0) = 1, ~~ y'(1) = 5 \end{matrix*} \right. \] sol: \(y(x) = x^4 +x\).

解:对方程做降阶处理：

\[ \left\lbrace \begin{matrix*}[l] y' = z; \\ z' = -xz + 4y + 12x^2 - 3x, \\ y(0) = S, ~~ z(0) = 1, \end{matrix*} \right. \]

%filename: chapter3_example_3_shooting_method.m
%用打靶法求解常微分方程的边值问题（第二类边界条件），其中用到了弦割法和四阶R-K算法。
function shooting_method_RK_secant
clear
clc
close all
format long

A=1;
x=0:0.001:A;
y=@(x)(x.^4+x); %方程的精确解;

DL=10^-15;    %误差判断标准，用于弦割法
XL=0.0;       %左边界点
XU=1.0;       %右边界点
h=0.02;           
N=(XU-XL)/h;
xx=0:h:N*h;
YL_D= 1.0;              %边界点导数值
YU_D= 5.0;              %边界点导数值
S0= 1000;                  %XL处函数猜测值，弦割法第一个启动点
S1= 2000;                  %第二个函数猜测值，作为弦割法的第二个启动点

% y_rk1=zeros(1,N+1);
% z_rk1=zeros(1,N+1);
% y_rk2=zeros(1,N+1);
% z_rk2=zeros(1,N+1);
% y_rk=zeros(1,N+1);
% z_rk=zeros(1,N+1);

%---------第一个试探解，求右边界的函数值及误差函数-------------------
f=@(xx,yy)[yy(2),-xx*yy(2)+4*yy(1)+12*xx^2-3*xx]; % 定义 f1，
z10 = [S0,YL_D]; 
z1 = myrungekutta(f, xx, z10);
y_rk1 = z1(:,1);   %用四阶RK算法求得的y值
z_rk1 = z1(:,2); 
F0=z_rk1(end)-YU_D; %用四阶RK算法得到的XU点的导数值与边界条件的差值
%----------第二个试探解，求右边界的函数值及误差函数--------------------
z20 = [S1,YL_D]; 
z2 = myrungekutta(f, xx, z20);
y_rk2 = z2(:,1);   %用四阶RK算法求得的y值
z_rk2 = z2(:,2); 
F1=z_rk2(end)-YU_D; %用四阶RK算法得到的XU点的导数值与边界条件的差值
D=min(abs(F1),abs(F0));
nn=0;
while(D>DL)
    S2=S1-F1*(S1-S0)/(F1-F0);
    S0=S1;
    S1=S2;
    F0=F1;
    nn=nn+1;
%----------第三或更高次的试探解，求右边界的函数值及误差函数--------------------
    z20 = [S1,YL_D]; 
    z2 = myrungekutta(f, xx, z20);
    y_rk2 = z2(:,1);   %用四阶RK算法求得的y值
    z_rk2 = z2(:,2); 
    F1=z_rk2(end)-YU_D; %用四阶RK算法得到的XU点的导数值与边界条件的差值
    D=min(abs(F1),abs(F0));
end
if (abs(F1)>abs(F0))
    y_rk=y_rk1;
    z_rk=z_rk1;
else
    y_rk=y_rk2;
    z_rk=z_rk2;
end

for a=0:h:N*h;
n=round(a/h);
error(n+1)=y(a)-y_rk(n+1);
end
fprintf('打靶法求得y(1)的导数值为：%f\n',z_rk(N+1));
fprintf('打靶法求得y(1)导数值的误差为：%f\n',YU_D-z_rk(N+1));
fprintf('打靶法的迭代次数为：%f\n',nn);

subplot(2,1,1),plot(x,y(x),'b',xx,y_rk,'r')%精确解
title('打靶法结果与精确解比较')
legend('精确解','打靶法','Location','best')
subplot(2,1,2),plot(xx,error,'r')  %打靶法误差曲线
title('打靶法误差曲线')
hold off

function z = myrungekutta(f, xx, z0)
n = length(xx);
h = xx(2)-xx(1);
z(1,:)=z0;
for i = 1:n-1
    k1 = f(xx(i), z(i,:));
    k2=f(xx(i)+0.5*h, z(i,:) + h*k1/2);
    k3=f(xx(i)+0.5*h, z(i,:) + h*k2/2);
    k4=f(xx(i)+h, z(i,:) + h*k3);
    z(i+1,:)=z(i,:) + (k1 + 2*k2 + 2*k3 + k4)*h/6;
end
Show the code 
def shooting(ode, x0, y0, h, xp, yp, eps):
    s1 = 0.1
    s2 = 0.2
    y00 = np.array([0.0, y0])
    while true:
        y00[0] = s1
        x1, y1 = rk4(ode, x0, y00, h, xp)
        y00[0] = s2
        x2, y2 = rk4(ode, x0, y00, h, xp)
        y11 = y1[:, 0]
        y22 = y2[:, 0]
        if (np.abs(y1[-1, 1] - yp) < eps):
            return x1, y11
        if (np.abs(y2[-1, 1] - yp) < eps):
            return x2, y22
        s3 = s2 - (s2 - s1) / (y2[-1, 1] - y1[-1, 1]) * (y2[-1, 1] - yp)
        y00[0] = s3
        x3, y3 = rk4(ode, x0, y00, h, xp)
        y33 = y3[:, 0]
        if (np.abs(y3[-1, 1] - yp) < eps):
            return x3, y33
        s1 = s2
        s2 = s3

def ode(x, y):
    res = y.copy()
    res[0] = y[1]
    res[1] = -x * y[1] + 4 * y[0] + 12 * x**2 - 3 * x
    return res

x0 = 0
xp = 1.0

y0 = 1.0
yp = 5.0

h = 0.02
eps = 1e-6

xx, yy = shooting(ode, x0, y0, h, xp, yp, eps)

plt.plot(xx, yy)
plt.xlabel('x')
plt.ylabel('y')
plt.show()

Show the code 
y_ex = xx**4.0 + xx
plt.plot(xx, y_ex[:, 0] - yy)
plt.xlabel('x')
plt.ylabel('err')
plt.show()

5 打靶法求本征值问题

考虑一根密度均匀的绷紧的弦的振动，

\[ \partial_t^2 u = c^2\nabla^2 u \longrightarrow \left\lbrace \begin{matrix*}[l] \partial_t^2 u(x, t) - c^2 \partial_x^2 u(x, t) = 0 \\ u(0, t) = 0; ~~ u(1, t) = 0; \end{matrix*} \right. \]

\[ \begin{matrix*}[l] u(x, t) = T(t)\phi(x) \\ \frac{T''(t)}{c^2T(t)} = \frac{\phi''(x)}{\phi(x)} \equiv = -k^2 \end{matrix*} \longrightarrow \left\lbrace \begin{matrix*}[l] T''(t) + c^2k^2T(t) = 0 \\ \partial_x^2 \phi = -k^2\phi \end{matrix*} \right. \]

分离变量后，空间部分满足的方程和边界条件可以写成 \[ \left\lbrace \begin{matrix*}[l] \partial_x^2 \phi = -k^2\phi; \\ \phi(0) = \phi(1) = 0 \end{matrix*} \right. \] \(k\) wavenumber, \(\phi\) transverse motion of the string.

Explicit solution: \[ \begin{matrix*}[l] k_n = n\pi; \\ \phi_n \sim \sin n\pi x;~~ (n = 1, 2, ...) \end{matrix*} \] 相比边值问题，本征值问题多了一个待定参数 —— 本征值

策略

先猜测一个试验本征值 \(k\)，同时任取一个非零参数\(\delta\)，把微分方程变化为一个初始值问题；

从 \(x = 0\) 向前递推产生一个数值解。如果该数值解在 \(x = 1\)处的值与边界条件 \(\phi(1) = 0\) 在误差范围内不相等，就改变试验本征值\(k\)的值，再度递推。重复这个过程，直到最终找到本征值和对应的本征函数。

注意：试验本征值 \(k\) 是一个可调参数(子弹)，而参数\(\delta\)只是一个任意选定的辅助参数，它的任意性是由于解的不唯一性引起的，并不影响本征值的求解，一般来说它可以由本征函数的归一化来确定。

与打靶法求解边值问题类似，求本征值\(k\) 的过程将成为一个方程求根过程。

此时Newton-Raphson法是不合适的，因为我们无法对要用数值方法确定的\(\phi(1)\) 值显式地对\(k\)求微分。

弦割法也是很危险的！ ❓ 🤔

因为方程有多个本征值，要控制迭代过程最终收敛到哪一个可能是困难的！

保险的做法是用简单搜索法（或二分法）确定一个本征值的近似位置，然后用效率更高的算法。

二分法的算法实现

给定有根区间 [a, b] ( f(a) f(b) < 0) 和 精度 \(\varepsilon\)

  1. 令 x = (a+b)/2
  2. 如果 b – a <\(\varepsilon\)，结束运算，输出 x
  3. 如果 f (a) f (x) < 0 , 则令 b = x，否则令 a = x, 返回第i步

%%{ init : { "theme" : "neutral", "flowchart" : { "curve" : "linear" }}}%%
flowchart TD

A["[a, b], s.t. f(a)f(b) < 0 && eps"]
B["let x = (a + b) / 2"]
C{"b - a < eps"}
D{"f(a)f(x) < 0"}
F("dump x")
G["a = x"]
H["b = x"]
A --> B --> C -->|false| D -->|true| H --> B
C -->|true| F
D -->|false| G --> B

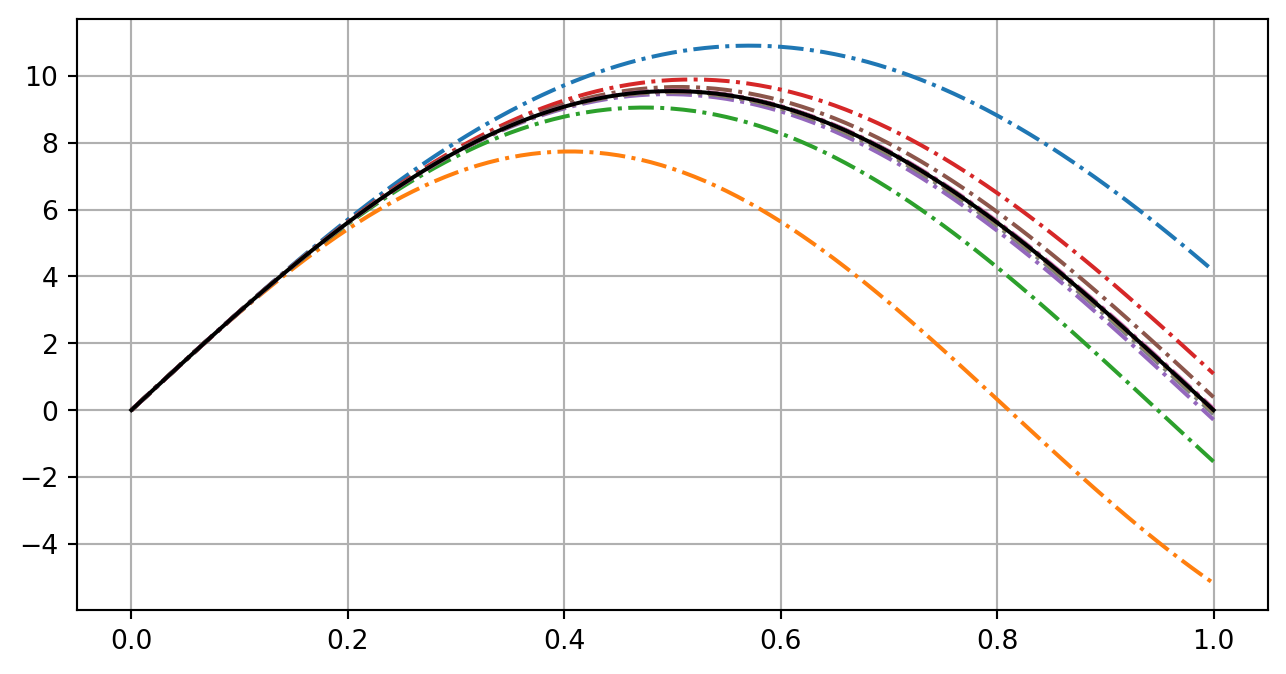
Example 4: 用打靶法求解上述紧绷弦问题的最小本征值。

\[ \left\lbrace \begin{matrix*}[l] \frac{d^2\phi}{dx^2} = -k^2\phi, \\ \phi(0) = \phi(1) = 0, \end{matrix*} \right. \longrightarrow \left\lbrace \begin{matrix*}[l] \frac{d^2\phi}{dx^2} = -k^2\phi, \\ \phi(0) = 0, \phi'(0) = \delta, \end{matrix*} \right. \tag{7}\]

降阶： \[ \left\lbrace \begin{matrix*}[l] \frac{d\phi}{dx} = z, \\ \frac{dz}{dx} = -k^2\phi, \\ \phi(0) = 0, \\ z(0) = \delta, \end{matrix*} \right. \tag{8}\]

%filename: chapter3_example_4_shooting_method_eigenvalue.m
%用打靶法求解常振动方程的本征值问题，其中用到了二分法和四阶R-K算法
%function shooting_method_RK
clear
clc;close all
format long

DL=0.5*10^-8;  %误差判断标准
XL=0.0;        %左边界点
XU=1.0;        %右边界点
N=100;           
h=(XU-XL)/N;
xx=XL:h:XL+N*h;
YL= 0.0;              %边界点函数值
YU= 0.0;              %边界点函数值
K1= 0.5;              %本征值猜测值，第一个
K2= 5;                %本征值猜测值，第二个,尝试5、10、20
delta=1.0;            %delta 为辅助参数

%---------第一个试探解，求右边界的函数值及误差函数-------------------
f1=@(xx,yy)[yy(2),-K1^2*yy(1)]; % 定义 f1，
z10 = [YL,delta]; 
z1 = myrungekutta(f1, xx, z10);
y_rk1 = z1(:,1);   %用四阶RK算法求得的y值
z_rk1 = z1(:,2); 
F1=y_rk1(end)-YU; %用四阶RK算法得到的XU点的函数值与边界条件的差值
%----------第二个试探解，求右边界的函数值及误差函数--------------------
f2=@(xx,yy)[yy(2),-K2^2*yy(1)]; % 定义 f1，
z20 = [YL,delta]; 
z2 = myrungekutta(f2, xx, z20);
y_rk2 = z2(:,1);   %用四阶RK算法求得的y值
%z_rk2 = z2(:,2); 
F2=y_rk2(end)-YU; %用四阶RK算法得到的XU点的函数值与边界条件的差值
D=min(abs(F1),abs(F2));
nn=0;
while(D>DL)
    nn=nn+1;
%----------二分法求误差方程的根-----------------
    if F1*F2>0.0
       fprintf('本征值不在两个输入点之间，程序终止');
        break;
    end
    K3=(K1+K2)/2.0;
    f3=@(xx,yy)[yy(2),-K3^2*yy(1)]; % 定义 f1，
    z30 = [YL,delta]; 
    z3 = myrungekutta(f3, xx, z30);
    y_rk3 = z3(:,1);   %用四阶RK算法求得的y值
%    z_rk3 = z3(:,2); 
    F3=y_rk3(end)-YU; %用四阶RK算法得到的XU点的函数值与边界条件的差值
    if F1*F3>0
       K1=K3;
       F1=F3;
       y_rk1=y_rk3;
    elseif F2*F3>0
       K2=K3;
       F2=F3;
       y_rk2=y_rk3;
    end
    D=min(abs(F1),abs(F2));
     plot(xx,y_rk3,'r', LineWidth=3)
     ylim([-0.2 0.5]);
     title('最小本征值对应的波函数', FontSize=20)
     M(nn)=getframe;
end
 movie(M,1,2)

if abs(F1)>abs(F2)
   y_rk3=y_rk2;
else
   y_rk3=y_rk1;
end
hold all
plot(xx,y_rk3,'r', LineWidth=3)
title('最小本征值对应的波函数', 'FontSize', 20)
fprintf('打靶法的迭代次数为：%f\n',nn);
fprintf('打靶法求得的本征值K为：%f\n',K3/pi,K3);


function z = myrungekutta(f, xx, z0)
n = length(xx);
h = xx(2)-xx(1);
z(1,:)=z0;
for i = 1:n-1
    k1 = f(xx(i), z(i,:));
    k2=f(xx(i)+0.5*h, z(i,:) + h*k1/2);
    k3=f(xx(i)+0.5*h, z(i,:) + h*k2/2);
    k4=f(xx(i)+h, z(i,:) + h*k3);
    z(i+1,:)=z(i,:) + (k1 + 2*k2 + 2*k3 + k4)*h/6;
end
end
Show the code 
eps = 1e-4
x0 = 0.0
xp = 1.0
h = 0.01

y0 = 0.0
yp = 0.0

def ode(x, y, k):
    res = y.copy()
    res[0] = y[1]
    res[1] = -k*k*y[0]
    return res

def shooting_evp(ode, x0, y0, h, xp, yp, eps):
    k1 = 0.5
    k2 = 5.0
    
    delta = 30.0
    y00 = np.array([y0, delta])
    
    node = lambda x, y: ode(x, y, k1)
    x1, y1 = rk4(node, x0, y00, h, xp)
    f1 = y1[-1, 0] - yp
    node = lambda x, y: ode(x, y, k2)
    x2, y2 = rk4(node, x0, y00, h, xp)
    f2 = y2[-1, 0] - yp
    
    if (f1 * f2 > 0):
        print("no roots in the interval")
        exit(1)
    if (f1 * f2 < 0):
            if (np.abs(k2 - k1) < eps):
                return 0.5 * (k1 + k2), xx, yy
        
    while True:
        kk = 0.5 * (k1 + k2)
        node = lambda x, y: ode(x, y, kk)
        xx, yy = rk4(node, x0, y00, h, xp)
        plt.plot(xx, yy[:, 0], '-.')
        if (np.abs(k2 - k1) < eps):
            return kk, xx, yy
        fx = yy[-1, 0] - yp
        if (f1 * fx < 0):
            k2 = kk
        else:
            k1 = kk
        node = lambda x, y: ode(x, y, k1)
        x1, y1 = rk4(node, x0, y00, h, xp)
        f1 = y1[-1, 0] - yp


kval, xval, yval = shooting_evp(ode, x0, y0, h, xp, yp, eps)
plt.grid('on')
plt.plot(xval, yval[:, 0], 'k-')
plt.show()

❓ 🤔 二分法求本征值只能求解单根！能否让程序求多根？

简单搜索法的算法实现

给定小于根的起始点\(a\)，步长\(h\)和 精度 \(\varepsilon\)

  1. 令 b = a+h;
  2. 如果 max(f(a),f(b)) < \(\varepsilon\)，结束运算，输出 b
  3. 如果 f (a) f (b) > 0 , 则令 a =b，否则令 h = h/2, 返回第1步

Example 4 用打靶法求解上述紧绷弦问题的前5个本征值, see (Equation 7), 降阶：(Equation 8).

%filename: chapter3_example_4_shooting_method_eigenvalue_2.m
%用打靶法求解振动方程的本征值问题，可以求多个本征值，
%其中用到了简单搜索法和四阶R-K算法;
function shooting_method_RK_secant
clear all
%close all
clc
format long

DL=0.5*10^-10;  %误差判断标准
XL=0.0;         %左边界点
XU=1.0;         %右边界点
N=1000;           
h=(XU-XL)/N;
xx=XL:h:XL+N*h;
YL= 0.0;              %边界点函数值
YU= 0.0;              %边界点函数值
K1= 0.0;              %本征值猜测值，第一个
dk=0.1;               %简单搜索法的初始步长
delta=100;           %delta为辅助参数，减小
mm=1;                 %要求的本征值的数目

for ii=1:mm
    nn=0;
    %---------第一个试探解，求右边界的函数值及误差函数-------------------
    f1=@(xx,yy)[yy(2),-K1^2*yy(1)]; % 定义 f1，
    z10 = [YL,delta]; 
    z1 = myrungekutta(f1, xx, z10);
    y_rk1 = z1(:,1);         %用四阶RK算法求得的y值
    F1=y_rk1(end)-YU;        %用四阶RK算法得到的XU点的函数值与边界条件的差值
    D=abs(F1);
    while(D>DL)
        nn=nn+1;
%----------第二个试探解，求右边界的函数值及误差函数--------------------
        K2=K1+dk;                %利用简单搜索法向前一步
        f2=@(xx,yy)[yy(2),-K2^2*yy(1)]; % 定义 f1，
        z20 = [YL,delta]; 
        z2 = myrungekutta(f2, xx, z20);
        y_rk2 = z2(:,1);         %用四阶RK算法求得的y值
        F2=y_rk2(end)-YU;    %用四阶RK算法得到的XU点的函数值与边界条件的差值

%----------简单搜索法求误差方程的根-----------------
        if F1*F2>0.0
           K1=K2;
           D=min(abs(F1),abs(F2));
           F1=F2;
        else
           K2=K2-dk;
           dk=dk/2;
           %D=min(abs(F1),abs(F2));
        end
    end
    hold on
   plot(xx,y_rk2)
   dk=0.1;  %dk恢复初值，搜索下一个本征值；
   K1=K2+dk;
    
   fprintf('打靶法的迭代次数为：%f\n',nn);
   fprintf('打靶法求得的本征值K为：%f\n',K2/pi);
end
    
function z = myrungekutta(f, xx, z0)
n = length(xx);
h = xx(2)-xx(1);
z(1,:)=z0;
for i = 1:n-1
    k1 = f(xx(i), z(i,:));
    k2=f(xx(i)+0.5*h, z(i,:) + h*k1/2);
    k3=f(xx(i)+0.5*h, z(i,:) + h*k2/2);
    k4=f(xx(i)+h, z(i,:) + h*k3);
    z(i+1,:)=z(i,:) + (k1 + 2*k2 + 2*k3 + k4)*h/6;
end

%filename: chapter3_example_4_shooting_method_eigenvalue_3.m
%用打靶法求解振动方程的本征值问题，可以求多个本征值，
%其中用到了简单搜索法（结合二分法）和四阶R-K算法.
function shooting_method_RK_bisection
clear all
close all
clc
format long

DL=0.5*10^-10;  %误差判断标准
XL=0.0;         %左边界点
XU=1.0;         %右边界点
N=1000;           
h=(XU-XL)/N;
xx=XL:h:XL+N*h;
YL= 0.0;              %边界点函数值
YU= 0.0;              %边界点函数值
K1= 0.0;              %本征值猜测值，第一个
dk=0.1;               %简单搜索法的初始步长
delta=300;           %delta为辅助参数
mm=5;                 %要求的本征值的数目

%hold on
for ii=1:mm
    nn=0;
%---------第一个试探解，求右边界的函数值及误差函数-------------------
    f1=@(xx,yy)[yy(2),-K1^2*yy(1)]; % 定义 f1，
    z10 = [YL,delta]; 
    z1 = myrungekutta(f1, xx, z10);
    y_rk1 = z1(:,1);              %用四阶RK算法求得的y值
    F1= y_rk1(end)-YU;            %用四阶RK算法得到的XU点的函数值与边界条件的差值  
    D=abs(F1);
    while(D>DL)
        nn=nn+1;
%----------第二个试探解，求右边界的函数值及误差函数--------------------
        K2=K1+dk;           %利用简单搜索法向前一步
        f2=@(xx,yy)[yy(2),-K2^2*yy(1)]; % 定义 f2，
        z20 = [YL,delta]; 
        z2 = myrungekutta(f2, xx, z20);
        y_rk2 = z2(:,1);              %用四阶RK算法求得的y值
        F2    = y_rk2(end)-YU;        %用四阶RK算法得到的XU点的函数值与边界条件的差值
%----------简单搜索法结合二分法求误差方程的根-----------------
        if F1*F2>0.0
           K1=K2;
           D=min(abs(F1),abs(F2));
           F1=F2;
        else
            D=min(abs(F1),abs(F2));
            while(D>DL)  %进入二分法循环
                nn=nn+1;
                K3=(K1+K2)/2;
                f3=@(xx,yy)[yy(2),-K3^2*yy(1)]; % 定义 f3，
                z30 = [YL,delta]; 
                z3 = myrungekutta(f3, xx, z30);
                y_rk3 = z3(:,1);   %用四阶RK算法求得的y值
                F3=y_rk3(end)-YU;  %用四阶RK算法得到的XU点的函数值与边界条件的差值
                if F3*F2>0.0
                    K2=K3;
                    F2=F3;
                else
                    K1=K3;
                    F1=F3;
                end   
                D=min(abs(F1),abs(F2));
            end   %结束二分法循环
        end
    end
   dk=0.1;
   K1=K2+dk;
   figure;plot(xx,y_rk3,'r')
   fprintf('打靶法的迭代次数为：%f\n',nn);
   fprintf('打靶法求得的本征值K为：%f\n',K2/pi);
end
%hold off

function z = myrungekutta(f, xx, z0)
n = length(xx);
h = xx(2)-xx(1);
z(1,:)=z0;
for i = 1:n-1
    k1 = f(xx(i), z(i,:));
    k2=f(xx(i)+0.5*h, z(i,:) + h*k1/2);
    k3=f(xx(i)+0.5*h, z(i,:) + h*k2/2);
    k4=f(xx(i)+h, z(i,:) + h*k3);
    z(i+1,:)=z(i,:) + (k1 + 2*k2 + 2*k3 + k4)*h/6;
end
Show the code 
eps = 1e-4
x0 = 0.0
xp = 1.0
h = 0.1

y0 = 0.0
yp = 0.0

def ode(x, y, k):
    res = y.copy()
    res[0] = y[1]
    res[1] = -k*k*y[0]
    return res

def shooting_evp(ode, x0, y0, h, xp, yp, eps, n):
  
    j = 1
    
    k1 = 0.0
    k2 = k1 + h
    
    delta = 30.0
    y00 = np.array([y0, delta])
    
    node = lambda x, y: ode(x, y, k1)
    x1, y1 = rk4(node, x0, y00, h, xp)
    f1 = y1[-1, 0] - yp
    node = lambda x, y: ode(x, y, k2)
    x2, y2 = rk4(node, x0, y00, h, xp)
    f2 = y2[-1, 0] - yp
    
    if (f1 * f2 > 0):
        k1 = k2
        k2 = k1 + h
    if (f1 * f2 < 0):
            if (np.abs(k2 - k1) < eps):
                print(j, kk)
                plt.plot(xx, yy[:, 0], label = 'k = ' + str(j))
                j = j + 1
        
    while j < n:
        kk = 0.5 * (k1 + k2)
        node = lambda x, y: ode(x, y, kk)
        xx, yy = rk4(node, x0, y00, h, xp)
        plt.plot(xx, yy[:, 0], '-.')
        if (np.abs(k2 - k1) < eps):
            print(j, kk)
            plt.plot(xx, yy[:, 0], label = 'k = ' + str(j))
            j = j + 1
            k1 = k2
            k2 = k1 + h
        fx = yy[-1, 0] - yp
        if (f1 * fx < 0):
            k2 = kk
        else:
            k1 = kk
        node = lambda x, y: ode(x, y, k1)
        x1, y1 = rk4(node, x0, y00, h, xp)
        f1 = y1[-1, 0] - yp


shooting_evp(ode, x0, y0, h, xp, yp, eps, 3)
plt.grid('on')
plt.legend()
plt.show()
1 0.199951171875
2 0.29995114803314216

6 Sturm-Liouville Problem

An important class of linear equations in physics is known as Sturm-Liouville problem, defined by \[ [p(x)u'(x)]' + q(x)u(x) = s(x) \] which has the first-order derivative term combined with the second-order derivative term.

Here, \(p(x), q(x)\) and \(s(x)\) are the coefficient functions of \(x\).

For most actual problems, \(s(x) = 0\) and \(q(x) = -r(x) + \lambda w(x)\), where \(\lambda\) is the eigenvalue of the equation, and \(r(x)\) and \(w(x)\) are the redefined coefficient functions.

The Legendre equation, the Bessel equation, and their related equation in physics are the examples of the Sturm-Liouville problem.

with \[ \Delta_1 = \frac{u_{i+1} - u_{i-1}}{2h} = u'_i + \frac{h^2 u_i^{(3)}}{3!} + O(h^4) \tag{9}\] and \[ \Delta_2 = \frac{u_{i+1} -2u_i + u_{i-1}}{h^2} = u''_i + \frac{h^2u^{(4)}_i}{4!} + O(h^4) \tag{10}\]

Multiply (Equation 9) by \(p'_i\) and (Equation 10) by \(p_i\) and add them together, we have \[ p'_i \Delta_1 + p_i \Delta_2 = \underbrace{(p_iu'_i)'}_{s_i - q_i u_i} + \underbrace{\frac{h^2}{12} \left(p_iu^{(4)}_i + 2p'_i u^{(3)}_i\right) + O(h^4)}_\text{remove all} \] Simplest numerical algorithm: \[ \rightarrow (2p_i + hp'_i)u_{i+1} + (2p_i - hp'_i)u_{i-1} = 4p_iu_i + 2h^2(s_i - q_iu_i) \]

Legendre equation

\[ \frac{d}{dx}\left[(1-x^2) \frac{du}{dx}\right] + l(l+1)u = 0 \] with \(l = 0, 1, \dots ,\infty\) and \(x \in [-1, 1]\). The solutions of the Legendre equation are the Legendre polynomials \(P_l(x)\).

\[ p(x) = 1-x^2; ~~~~ q(x) = l(l+1); ~~~~ s(x) = 0; \]

\[ \begin{eqnarray} \Rightarrow & &\left[2(1-x_i^2) + h (-2x_i)\right]u_{i+1} + \left[2(1-x_i^2) - h(-2x_i)\right]u_{i-1} \\ &=& 4\left[(1-x_i^2) - 2h^2l(l+1)\right]u_i \end{eqnarray} \]

\[ \Rightarrow u_{i+1} = \alpha_i \left[\beta_i u_{i} + \gamma_{i}u_{i-1}\right] \] with \[\alpha_i \equiv \frac{1}{2p_i + hp'_i} = \frac{1}{2(1-x_i^2) + h(-2x_i)},\] \[\beta_i \equiv 4p_i - 2h^2 q_i = 4\left[(1-x_i^2) - 2h^2l(l+1)\right],\] \[\gamma_i \equiv 2p_i - hp'_i = \left[2(1-x_i^2) - h(-2x_i)\right].\]

Assume we don’t know the value of \(l\) but the first two points of \(P_l(x) = x\); then we can treat the problem as an eigenvalue problem.

Show the code 
import numpy as np
import matplotlib.pyplot as plt
def simple_solve(x, y0, p, p1, l, s):
    res = np.zeros(x.shape)
    res[0] = y0[0]
    res[1] = y0[1]
    h = x[1] - x[0] 
    q = l * (l + 1.0)
    alpha = 1.0 / (2.0 * p + h * p1)
    beta = 4.0 * p - 2.0 * h**2 * q
    gamma = h * p1 - 2.0 * p
    s0 = 2*h**2 * s
    for i in range(1, len(x) - 1):
        res[i+1] = alpha[i] * (beta[i] * res[i] + gamma[i] * res[i-1] + s0[i])
    return res


def ieqn(l):
    nn = 101
    x = np.linspace(0.0, 1.0, nn)
    h = x[1] - x[0]
    p = (1.0 - x**2.0)
    p1 = -2.0 * x
    s = np.zeros(x.shape)
    y0 = np.array([0.0, h])
    res = simple_solve(x, y0, p, p1, l, s)
    return res[-1] - 1.0


def root_find(l0, dl, ln, leps):
    inn = 0
    l00 = l0
    l01 = l0 + dl
    result = np.zeros(ln)
    while inn < ln:
        f0 = ieqn(l00)    
        f1 = ieqn(l01)
        #print("%6.5f\t%6.5f\t%6.5f\t%6.5f" %(l00, l01, f0, f1))
        if (f0 * f1 > 0):
            l00 = l00 + dl
            l01 = l00 + dl
        else:
            if (np.abs(l01 - l00) < leps):
                result[inn] = 0.5 * (l00 + l01)
                inn += 1
                l00 = l01
                l01 = l01 + dl
            else:
                temp = 0.5 * (l00 + l01)
                f1 = ieqn(temp)
                if (f0 * f1 > 0):
                    l00 = temp
                else:
                    l01 = temp
    return result

l0 = 0.5
dl = 0.1
ln = 3
leps = 1e-10

result = root_find(l0, dl, ln, leps)
print(result)
[ 1.         36.48417442 37.60636423]

7 Seminar: Schodinger equation

Back to top